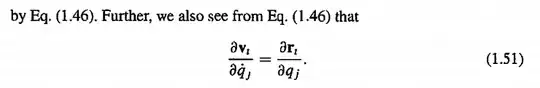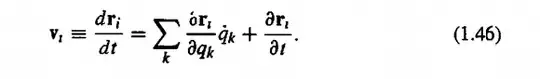(I could not find any answer to the following question in other related questions posted on SE, so asking it here.)
In the derivation of D'Alembert's principle in his "book", Goldstein uses the relation,
Where the set {ri} is the set of cartesian coordinates used to describe the configuration of a given system and {qi} is the set of independent coordinates such that each ri can be expressed in terms of qi's. i.e. ri=ri(q1,q2,.......,t) where 't' is time. vi is given by the equation,
Now, my question is how is the expression (1.51)(given in the first image) obtained? I tried to directly differentiate the expression of vi, but it will give another term on the RHS of (1.51). I tried to find out on google, and I got "this" pdf which also agrees with my doubt.