Method of image charges for more than one surface

Question

I would like to better understand the method of image charges for more than one planar surface. I know that the whole objective is to satisfy the boundary conditions, and thus this can be used as a check for any potential solution. However I would like to know if there are a consistent set of rules for applying the "Method of Image Charges" rather than making reasonable guesses and then checking the solutions are correct.

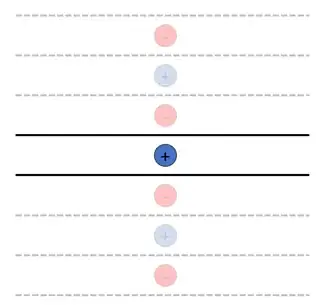
For example, I know that the solution to a point charge between two infinite planes is as follows. Using the Method of Image Charges for the upper plane dictates that you place an opposite charge symmetrically on the other side. You then turn your attention to the other plane. It now has two charges above its surface and the Method of Image Charges dictates that you place two opposite charges symmetrically on the other side etc. etc. until you have an infinite ladder of charges. See image below (where reflections extend to infinity).

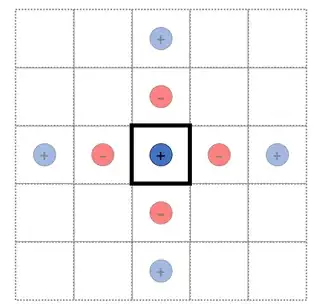
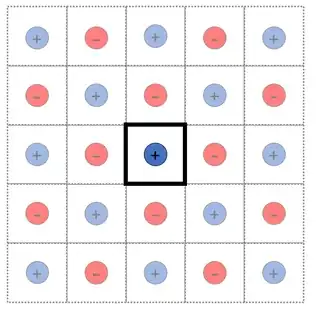
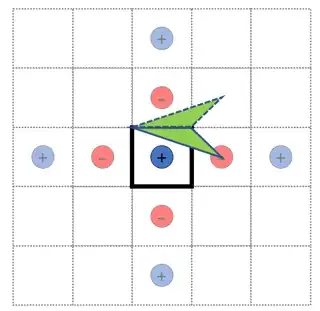
However for more than one planar surface, particularly finite surfaces, I am not sure how to consistently apply the Method of Image Charges. For example, consider a point charge in a box. Just applying the Method, one could envisage a solution such as (A) below. It's basically two copies of the previous example. On the other hand, a solution like (B) also seems reasonable, because you reflect the solutions from one set of planes around the perpendicular planes. The confusion comes for me in the fact that the planes are not infinite. I am not sure if the Method of Image Charges clearly dictates which answer is correct, without resorting to checking the boundary conditions are satisfied (although this is of course a sensible check). I am ultimately interested in this question because I am modelling an array of interacting dipoles in a photonic cavity (and I assume perfect metallic boundary conditions for simplicity of the model).

Option (A)

Option (B)

Answer 1

In my experience these are usually ingeniously guessed solutions. Solutions for two surfaces are usually already quite complex, since one has to build images of images, and the number of these images quickly becomes infinite.

Note also that the method of images is also used beyond electrostatics, e.g., for duffusion problem.

Answer 2

I think I have found the correct answer. My reasoning is as follows. We can quickly check that (B) is the correct answer. Pick any random image charge. Consider all the vectors from that charge to one of the boundaries. The span of these vectors gives us a triangle. For the potential at this boundary to be zero we need to balance the image charge with an opposite (image) charge at a location where the length of all the vectors in that triangle are the same. The only way to do this is to 'reflect the triangle' along the boundary. In (A) we can easily find an unbalanced charge. In (B) we can see that all charges are balanced.

Option (A)

Option (B)

Analytical verification of solution

Set the origin at the location of the real charge. Use dimensions such that the square is a unit square. Then the potential due to the charges in (B) is

$$V(x,y) = \sum_{m,n\in \mathbb{Z}}(-1)^{m+n}\left[ (x+m)^2 + (y+n)^2 \right]^{-1/2}$$

We can check the potential at the right wall equals zero

\begin{aligned} V(1/2,y) &= \sum_{m,n\in \mathbb{Z}}(-1)^{m+n}\left[ (1/2+m)^2 + (y+n)^2 \right]^{-1/2}\\ &= 2 \sum_{n\in \mathbb{Z}}(-1)^n\sum_{m\in \mathbb{Z}}(-1)^m\left[ (1+2m)^2 + (2y+2n)^2 \right]^{-1/2}\\ &= 2 \sum_{n\in \mathbb{Z}}(-1)^n\sum_{m\in \mathbb{Z}}(-1)^m f(m,n)\\ \end{aligned}

where $f(m,n)=\left[ (1+2m)^2 + (2y+2n)^2 \right]^{-1/2}$. We can split the sum over integer $m$ into two sums; one over the natural numbers (including zero) and one over the negative integers.

$$\sum_{m\in \mathbb{Z}}(-1)^m f(m,n) = \sum_{m\in \mathbb{N}_0}\left[(-1)^m f(m,n) - (-1)^m f(-m-1,n) \right]$$

It is easily verified that $f(m,n)=f(-m-1,n)$, and thus the above sum equals zero.