Kirchhoff's diffraction law (optics),
 \begin{align}
U(P_0) &= \int_\Sigma U^{\prime}(P_1) \frac{\exp(i kr_{01})}{r_{01}} dS
\\
U^{\prime}(P_1) &=\frac{1}{i\lambda} \cdot
A\frac{\exp(i kr_{02})}{r_{02}}\cdot
\frac{\cos{(\varphi_{n1})} - \cos{(\varphi_{n2})}}{2}
\end{align}
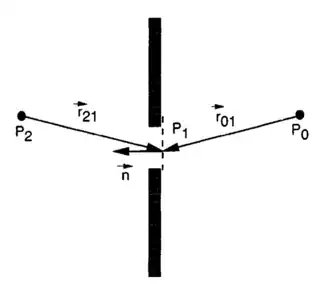
where a point-source is located at position $P_2$ and we measure the (scalar) field at position $P_1$, can be understood as the superposition of spherical waves located inside the region of the aperture $\Sigma$ with the phase factor $U^{\prime}(P_1)$. I'm interested in the
"projection factor" (so called inclination factor)
$$
\cos{(\varphi_{n1})} - \cos{(\varphi_{n2})}
= \cos{(\vec{n}, \vec{r}_{01})} - \cos{(\vec{n}, \vec{r}_{02})}
$$
where $\varphi_{n1}$ is the angle between the $\vec{r}_{01}$ and the normal direction of the aperture, $\vec n$ (and analog for $\varphi_{n2}$).
\begin{align}
U(P_0) &= \int_\Sigma U^{\prime}(P_1) \frac{\exp(i kr_{01})}{r_{01}} dS
\\
U^{\prime}(P_1) &=\frac{1}{i\lambda} \cdot
A\frac{\exp(i kr_{02})}{r_{02}}\cdot
\frac{\cos{(\varphi_{n1})} - \cos{(\varphi_{n2})}}{2}
\end{align}
where a point-source is located at position $P_2$ and we measure the (scalar) field at position $P_1$, can be understood as the superposition of spherical waves located inside the region of the aperture $\Sigma$ with the phase factor $U^{\prime}(P_1)$. I'm interested in the
"projection factor" (so called inclination factor)
$$
\cos{(\varphi_{n1})} - \cos{(\varphi_{n2})}
= \cos{(\vec{n}, \vec{r}_{01})} - \cos{(\vec{n}, \vec{r}_{02})}
$$
where $\varphi_{n1}$ is the angle between the $\vec{r}_{01}$ and the normal direction of the aperture, $\vec n$ (and analog for $\varphi_{n2}$).
I understand how this factor is mathematically derived. I also know that two terms can be combined and we obtain a single $cos$-function (Rayleigh-Sommerfeld diffraction). However, I am missing the intuition. How can the inclination factor be motivated? What is the intuitive picture behind the projection?
My wrong intuition is: We have a spherical wave, thus, we don't have to consider directions. The phase due to the exponent $k r_{01}$ takes care oft everything.