Why are charged pions are heavier than neutral pions?

Question

Why are charge pions heavier than neutral pions, whereas protons are lighter than neutrons?

Answer 1

As anna v says, hadrons are really complicated and you're not going to be able to do a full calculation without a lot of computer time. But you can get at least an idea by thinking about the quark model. The proton is $uud$, the neutron is $udd$, the $\pi^+$ is $u\bar{d}$ and $\pi^0$ is $\frac{1}{\sqrt{2}}(u\bar{u} - d\bar{d})$ (the - sign so that it's an isospin triplet). The charge of the up quark is $+\frac{2}{3}$, and the charge of the down quark is $-\frac{1}{3}$. Their "current masses" are $m_u=2.2$ MeV and $m_d=4.7$ MeV (I'm not bothering with the uncertainties on these). If the up and down quarks had the same mass, and if we could turn off the electromagnetic interaction, then protons and neutrons would have the same mass, and charged and neutral pions would have the same mass. But they don't, and we can't, so they don't.

Now, let's look at the pions. The contribution of the quark masses to the $\pi^+$ mass is $m_u+m_d = 6.9$ MeV (the antiquarks have the same masses as the quarks), and the contribution to the $\pi^0$ mass is $\frac{1}{2}(2\times 2.2 + 2\times 4.7)=6.9$ MeV. (Note that this is nowhere near enough to explain the full mass of the pion. For that you need a full QCD calculation. But it is relevant for understanding the mass difference.) The contribution of the quark masses is the same in both pions, so the difference is most likely due to electromagnetic effects. In this case, we expect the charged pion to have some self-repulsion and so have a larger mass. As a rough estimate, the electrostatic energy of a uniformly-charged sphere of charge $Q$ and radius $r$ is $U=\frac{3}{5}\frac{Q^2}{r^2}$. The charge radius of the pion is something like 0.66 fm, so plugging in the numbers gives roughly 2 MeV, which is at least the right order of magnitude to explain the pion mass difference of 4.4 MeV.

Now to the nucleons. The contribution of the quark masses to the proton mass is $2\times 2.2 + 4.7=9.1$ MeV, and the contribution of quark masses to the neutron mass is $2.2 + 2\times 4.7=11.6$ MeV. Here we see that the neutron gets more contribution from quark masses (by 2.5 MeV) because it has more $d$ quarks. But the proton is charged, and so should have some electrostatic repulsion. Taking a charged sphere with radius $r=0.84$ fm, this gives an electrostatic repulsion of 1.2 MeV. So combining the 2.5 MeV excess for the neutron due to quark masses with the 1.2 MeV excess for the proton due to electrostatic repulsion suggests that the neutron should be heavier by 1.3 MeV.

This just so happens to be about the right value, but this was a very hand-waving calculation. At least it gives an idea of how the mass differences could come out as they do.

Answer 2

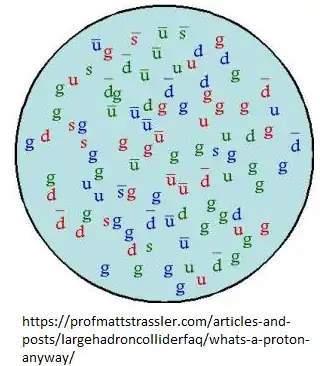
Look at this illustration of the proton to get an idea of how complicated a hadron is.

There are the valence quarks that define the quantum numbers of the particles but the greatest effect on the mass comes from the additions of the innumerable four vectors of all those sea particles, up an down quarks have small masses and in addition in the bag of the hadron all quarks are off mass shell and obey quantum mechanical probability constraints.

So the answer is not simple. As you note , neutrons are heavier than protons, and the same is true for neutral kaons with respect to charged. The Sigma baryons, have small mass differences and their study could help to show which effects are dominant in determining the mass.

I believe the answer can only come through calculations, taking into account all factors, electromagnetic and strong. The masses of hadrons are an ongoing research in QCD on the lattice. , and maybe someday there will be a calculated answer for this behavior of pions.