How to prove that $u(r)=k \dfrac{1}{r}$ is the only solution for the integral equation $\displaystyle\int_{V'}\rho'\ u(r)\ dV' = constant$?

Question

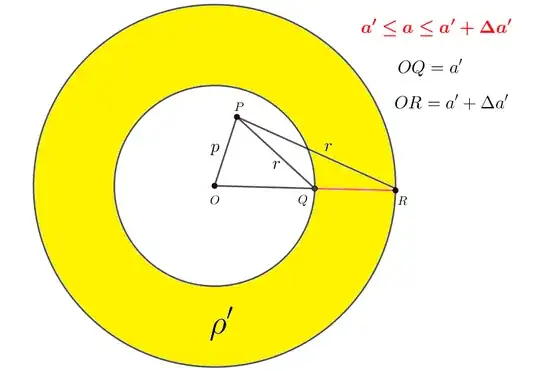
Consider a hollow spherical charge with density $\rho'$ continuously varying only with respect to distance from the center $O$.

$V'=$ yellow volume

$k \in \mathbb {R}$

$\forall$ point $P$ inside the hollow sphere:

\begin{align} \vec{E}_P &=\displaystyle\int_{V'}\rho'\ \vec{f}(r)\ dV'\\ &=\int_{V'}\rho'\ [-\nabla u(r)]\ dV'\\ &=-\nabla \int_{V'}\rho'\ u(r)\ dV' = 0\\ \implies \int_{V'}\rho'\ u(r)\ dV' &= constant\\ \implies u(r) &=k \dfrac{1}{r}\\ \end{align}

For the proof of last equation, see below:

1. The converse of Newton's shell theorem

2. https://math.stackexchange.com/questions/3592927/logically-deducing-inverse-square-law-physics?answertab=votes#tab-top

3. https://www.docdroid.net/Wg59yXo/v-pdf

How shall we prove that $u(r)=k \dfrac{1}{r}$ is the only solution for the integral equation $\displaystyle\int_{V'}\rho'\ u(r)\ dV' = constant$?

The following article is from [wikipedia Shell theorem]. Read the grey highlighted text(https://en.wikipedia.org/wiki/Shell_theorem#Converses_and_generalizations)