3

According to this page https://www.nanoscience.com/techniques/quartz-crystal-microbalance/,

“AT cut” provides pure thickness shear mode oscillation where the two surfaces of the crystal move in an anti-parallel fashion.

How can I model and derive this result mathematically? I guess I would have to make and solve wave equations considering piezoelectric effect in quartz crystal, but I am lost where I should start. Any reference or help are appreciated.

enter image description here enter image description here

GouldBach
  • 175

2 Answers2

2

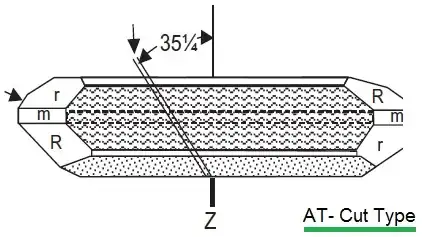
Although I have not derived any of these equations, I can safely say that you will find a beginning of an answer in a book by Royer and Dieulesaint, Elastic waves in Solids volume 1, section 4. I'm pretty sure to find a definite answer, you'll have to solve the specific Christoffel equation. I think it has to do indeed, as pointed out by Jon Custer, to the crystal orientation and symmetry. (As defined by standards IEEE 176-1978) the AT cut has angles $\theta = 35$ deg and $\varphi = 0$. The angles are defined as:

  1. $\varphi$ is the first rotation aroud axis Z in the crystalline structure, giving axes $X^\prime$, $Y^\prime$ and $Z^\prime=Z$.
  2. $\theta$ is the angle of the second rotation aroud axis $X^\prime$

Another reference you might want to check is An analysis of doubly rotated quartz resonators utilizing essentially thickness modes with transverse variation by Stevens and Tiersten, you may find useful information there. Hope you find any useful information in these references

elkevn
  • 41
0

"The Quartz Crystal Microbalance in Soft Matter Research: Fundamentals and Modeling" by Diethelm Johannsmann has a chapter dedicated to modeling QCM as a parallel plate. If you are interested in the application aspects of QCM, I highly recommend this book.

thomas
  • 21
  • 3