0

How can buoyant force be derived from most basic laws of fluids ?
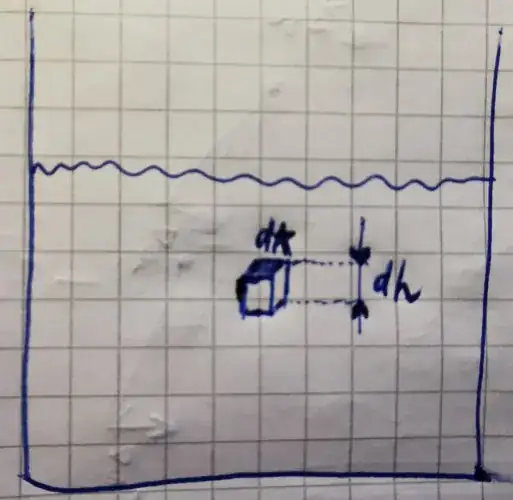
I can think of easy one. Consider such scheme of body floating deep in water :

enter image description here

Where $dA$ is elementary downward directed surface unit of a body, $dh$ - elementary change of depth.

Then infinitesimal pressure change by definition is : $$ dp = \rho g\, dh $$

Pressure is force per unit area, substituting this into formula gives, $$ \frac {dF}{dA} = \rho g\, dh $$

Moving elementary surface into right side of equation gives,

$$ dF = \rho g\, dA\, dh $$

Further we notice that $dA \cdot dh$ is nothing but elementary volume, so we can rewrite equation as :

$$ dF = \rho g \,dV $$

Now we need to integrate both sides of equation,

$$ \int dF = \int \rho g \,dV$$

Which further integrating elementary volume against floating in water body part $V_f$, gives :

$$ F = \rho g \int^{V_f}_0 dV = \rho g V_f $$

which is exactly buoyant force.

Any other buoyant force derivations from basic principles ?

Agnius Vasiliauskas
  • 16,916

1 Answers1

6

We will need the following two facts:

  • In hydrostatic equilibrium, the distribution of pressure $P$ in a fluid is governed by the relation $$ \tag{$\ast$} \vec\nabla P=\rho\vec g, $$ where $\rho$ is the fluid density and $\vec g$ is the force per unit mass of the fluid due to any external field. (It does not have to be gravity, and it does not have to be homogeneous.)
  • The Gauss theorem of vector calculus in the form $$ \tag{$\ast\ast$} \int_{\partial V}\phi\,d\vec S=\int_V(\vec\nabla\phi)\,dV, $$ where $\phi$ is a scalar field, $V$ is a chosen domain in space and $\partial V$ its boundary, oriented so that the area element $d\vec S$ points out of $V$.

Let us now think of $V$ as some object immersed in the fluid and calculate the total force due to the pressure of the fluid on the object, $$ \vec F=-\int_{\partial V}P\,d\vec S=-\int_V(\vec\nabla P)\,dV=-\int_V\rho\vec g\,dV. $$ The last expression is exactly minus the total force by which the external field $\vec g$ would act on the body of fluid filling the volume $V$. This is the Archimedes principle.

All this said, I should add that one can use pretty much the same argument to actually derive $(\ast)$. This reflects the fact that one does not really need any mathematics to understand the Archimedes principle: by arguing that the force on the immersed object is the same as the force on the body of fluid filling the volume $V$ and invoking the condition of hydrostatic equilibrium, one arrives at the same conclusion immediately. Note that even the mathematical derivation shown here implicitly assumes that one can replace the object with the fluid filling the same volume $V$ without disturbing the surrounding fluid. This is hidden in the assumption that the field $P$ can be extended to the inside of $V$, and also there $(\ast)$ still holds.

One can of course derive $(\ast)$ in a similar way as you did, by choosing $V$ as an infinitesimal cube. The above maths can then be thought of as a mathematical derivation of the Archimedes principle for domains of arbitrary shape. Finally, those who prefer physics intuition to mathematical manipulations can think of the above as a "physical proof" of the Gauss theorem $(\ast\ast)$. You choose which interpretation you prefer!

Tomáš Brauner
  • 2,062