How to formalize taking line integral by a reversible or irreversible path?

Question

In thermodynamics work can be done by moving alone a reversible or irreversible path. Physical definitions of reversible and irreversible processes is uncommon in thermodynamics textbooks. The main idea is that I have to imagine something I can't. It is better to work with formal things than try to imagine. Work is line integral of differential form, $$W=\int_{L} P(x, y, z) dx+Q(x, y, z) dy+R(x, y, z) dz\tag{1}.$$ where $L$ is the equation of the curve. Does this mean that some curves $L$ have the property of being reversible paths and some don't? What does taking a line integral alone a reversible path mean mathematically? How can I formalize it?

Answer 1

Does this mean that some curves have the property of being reversible paths and some don't?

Yes. The work done by a reversible process between the same two equilibrium states will be greater than for the same process carried out irreversibly between the same two equilibrium states. Each has a different shape "curve" between the start and end points.

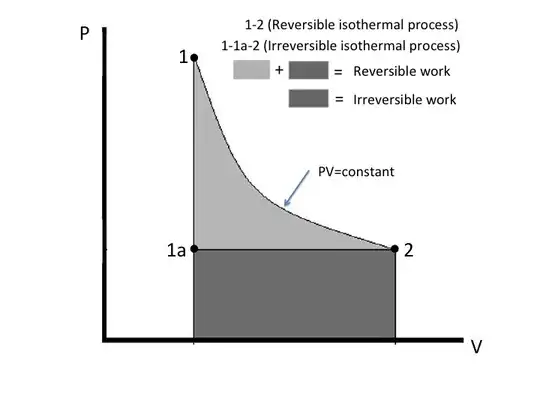
For a closed system the work of interest is called "pdV" work and the work between two states is $\int pdV$. The diagram below shows two different paths (or "curves" as you call them) between equilibrium states 1 and 2. Path 1-2 is for a reversible isothermal process. That's a process carried out very slowly gradually reducing the external pressure while the gas expands so the temperature of the ideal gas is constant (pV=constant) while it gradually takes in heat from the surroundings and performs an equal amount of work.

Path 1-1a-2 is an irreversible isothermal process. The external pressure is abruptly reduced from P1 to P1a and then the gas allowed to expand to the same final state 2. Although the temperature at the interface between the gas and surroundings is constant, there are temperature and pressure gradients within the gas that makes the process irreversible.

Note that the work done ($\int pdv$), or area under the curve, for path 1-2 is greater than that for path 1-1a-2. The difference is the light gray shaded area.

Hope his helps.

Answer 2

The way I see it, thermodynamical variables like $p$ and $T$ are only really defined in equilibrium. So when you draw curves in the $pV$ plane, you are implicitly saying that the process is quasistatic. Whether a quasistatic process is reversible or not is a confusing issue (to me); in the purest of situations it will be, but it depends on what happens in the environment (see here). So every curve $L$ has at least the potential to describe a reversible process. There is no such thing as an inherently irreversible curve.

A general irreversible process will start and end in equilibrium states (points on the $pV$ diagram), but will go through nonequilibrium states to get there. That will look like a "jump" between two points on the diagram, with no curve connecting them. To calculate properties like work and entropy change of irreversible processes, you need some additional information about what's happening during the process. For example, in the example by Bob D, it's not that the system actually goes along the full vertical and horizontal lines of constant $V$ and $p$, but rather that it somehow goes from 1 to 1a under constant volume, and then somehow on to 2 under constant external pressure (even though the "internal pressure" $p$ is not defined). This allows you to compute the work as $W = p_\mathrm{ext} \Delta V$ even though you can't write $\Delta V = \int dV$ along a nice curve of equilibrium states.

Apologies if that sounds a bit rambling.