2

I understood the concept of cross product with an example of Torque. I understood the concept. But what confuses me is that how can cross product of two orthogonal vector in a plane give us the product which is in other axis. i × j =k, how is that possible.

Eg:- This is a spinner.

enter image description here

Suppose we apply a perpendicular force and we multiply it with r so we get the torque (vector product). The spinner starts spinning.

enter image description here

So in this spinning picture how is there a motion or vector in 3rd dimension (k^), as the vector product theory suggests?

Qmechanic
  • 220,844
User
  • 366

2 Answers2

4

It's really just a convention that happens to work out nicely.

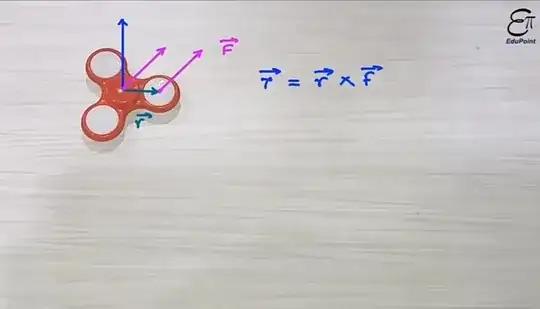
Fundamentally, rotations should be thought of as acting in a plane. For example, your spinner is rotating in the $xy$-plane. If you apply a force in the $x$-direction at a point on the $y$-axis, this exerts a torque in the $xy$-plane, and its angular momentum in the $xy$-plane changes.

Thought of this way, the torque isn't really the same as the vectors you learn about in intro physics. Among other things, it has two directions associated with it, rather than the single direction associated with a vector. And if you're an introductory student, it might be annoying & frustrating to have to learn a whole new set of mathematical machinery to do rotational motion. Vectors can be tricky enough!

But fortunately, there's a bit of a "hack" that we've come up with to get around this. If you think about it, saying that "this object is rotating in the $xy$-plane" is equivalent to saying "this object's $z$-axis is fixed." What the cross product does is to map the two vectors defining a rotation plane ($\hat{\imath}$ and $\hat{\jmath}$) to a vector defining the fixed axis ($\hat{k}$). There's not necessarily any motion in the $z$-direction when this happens; it's just a way of mapping rotation planes (such as the $xy$-plane) to rotation axes (such as the $z$-axis.)

Michael Seifert
  • 54,357
2

There is no motion in the third direction. The torque in three dimensions will be a vector if it satisfies the properties of a vector. From the way it adds and subtracts, from the way it transforms under changes of coordinate system, and by its behaviour under composition with other vectors using vector operations, we can conclude that it is a vector, and find its direction. For example, we can find the dot product of the torque with a vector in the i-j plane. If this vanishes, we can conclude that torque points in the $\pm$k direction.

Also, torque need not always be a vector, like in the hypothetical case of a two-dimensional world. We have rotations here, but no third direction, so torque is no longer a vector, since it just does not satisfy the properties of a two dimensional vector.

NewUser
  • 679