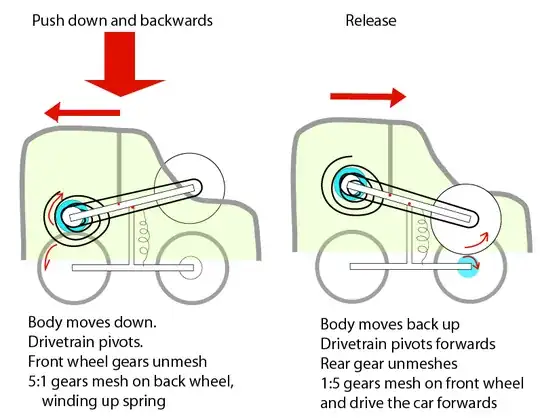
Are you are expecting that if you roll the car backwards $30\ \mathrm{cm}$ then release it, it should move forward $30\ \mathrm{cm}$? Why? Most toy cars wouldn't move at all.
If you put a stone in a catapult, pull it back $30\ \mathrm{cm}$ then release it, it goes forward much further than $30\ \mathrm{cm}$. If you did this in empty space the stone would keep going indefinitely.
Energy hasn't been created out of nothing. You have done work against the catapult, storing elastic energy. When you release the catapult the stored elastic energy is transformed into the kinetic energy of the stone, which is dissipated as heat and sound as the stone flies through the air and hits a target. If there is no air resistance or friction, and nothing impedes the stone, its kinetic energy remains constant forever – its speed doesn't change, it goes infinitely more than $30\ \mathrm{cm}$.
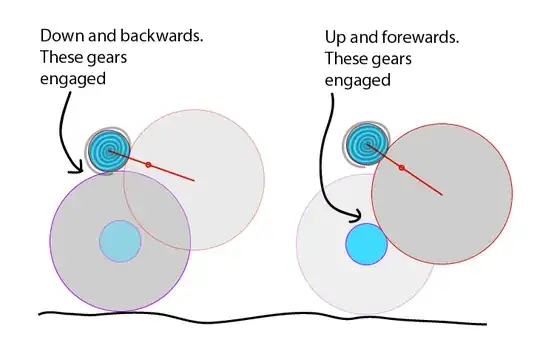
The toy car is the same. Instead of an elastic band, it contains a spring. Pushing down engages a gear wheel. As you push the toy car backwards you wind up the spring quickly using a relatively large force. You do work, elastic energy is stored in the spring. When the car is released, it springs back up and a different gear wheel is engaged. Now the spring unwinds itself slowly, supplying a much smaller force to the toy car. (See Note.) Elastic energy is transformed into the kinetic energy of the car, which is dissipated by friction. The car loses its kinetic energy gradually; it slows down and stops. If there was no friction the car would keep going indefinitely on a flat surface.
It is not the distances which you need to compare but the work done, which is force times distance. You give the car elastic potential energy by pushing with a large force over a short distance. The much smaller force of friction takes that energy away over a much longer distance after it has been transformed into kinetic energy.
Suppose the friction force is $0.1\ \mathrm N$ and you push the car backwards with a force of $5.1\ \mathrm N$ through a distance of $30\ \mathrm{cm}$. Then you have done $5.1\ \mathrm N \times 0.3\ \mathrm m = 1.53\ \mathrm{Nm}$ of work. Friction works in both directions so $0.1\ \mathrm N \times 0.3\ \mathrm m = 0.03\ \mathrm{Nm}$ of the work you do is wasted pushing against friction. The remaining $1.50\ \mathrm{Nm}$ of energy gets stored in the spring. When the car is released it is transformed into the kinetic energy of the car. The friction force of $0.1\ \mathrm N$ slows the car. You can expect the car to go a distance of $15\ \mathrm m$ before stopping because $0.1\ \mathrm N \times 15\ \mathrm m = 1.5\ \mathrm{Nm}$.
The car goes $50$ times further forwards than you moved it backwards. But you haven't created any energy. In fact, some energy was lost pushing against friction. Only $1.50\ \mathrm{Nm}$ of the $1.53\ \mathrm{Nm}$ of energy which you supplied was used to move the car forward.
Note: When the spring is fully unwound it is disengaged from the wheels so that the car rolls forward freely instead of winding the spring back up. That's like the catapult which releases the stone; otherwise the stone would stretch the elastic again and keep oscillating until its kinetic energy was used up.
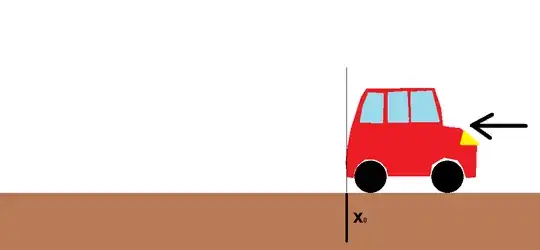
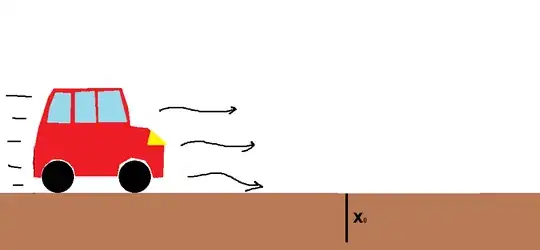
 Let's say, that the distance you have pushed the car is $d_1$ and the distance the car has travelled is $d_2$.
Let's say, that the distance you have pushed the car is $d_1$ and the distance the car has travelled is $d_2$.