Feynman Lectures: 20–3 The gyroscope

Question

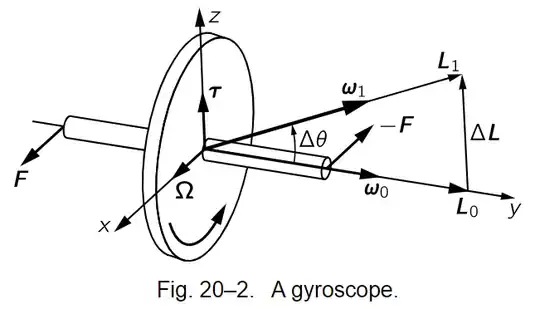
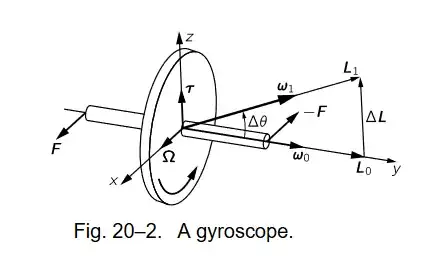
In the The Feynman Lectures on Physics, Volume I, Chapter 20, Section 3,The Gyroscope found here, Feynman wrote

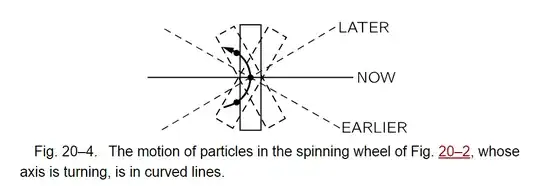
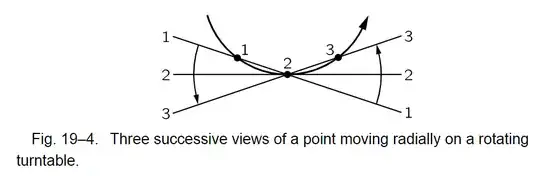
We note that when the wheel is precessing, the particles that are going around the wheel are not really moving in a plane because the wheel is precessing (see Fig. 20–4). As we explained previously (Fig. 19–4), the particles which are crossing through the precession axis are moving in curved paths, and this requires application of a lateral force. This is supplied by our pushing on the axle, which then communicates the force to the rim through the spokes.

Can someone please explain how the forces $F$ applied in Fig. 20-2 are lateral? I would have thought that the lateral force needed to be applied along the y-axis instead of the z-axis in order to supply the force needed to make the particle travel in the curve shown in Fig. 20-4 similar to Fig. 19-4. I can't figure out what this has to do with the Coriolis-effect which Fig. 19.4 is demonstrating.

Answer 1

I can’t see the numbered figures, so let me walk you through a slightly different physical example: a helicopter rotor.

Imagine the rotor is turning counterclockwise views from above. A rotor blade goes from “ahead” to “left” to “behind” to “right”.

Now imagine you provide an impulse down on a blade tip at the front, up on a blade at the back. Normally, you’d expect the rotor to move down at the front, up at the back: tilt forward.

But note what’s really happening: the impulse is a force for a time, which is a velocity change. Only after a time will it become a position change.

So when the rotor is turning, the blade is moving right to left at the front. The impulse adds a small downward component to the large right-left speed: the blade tip starts moving on the diagonal. It doesnt move down right at the front. It starts moving down, but only gets down by the time the rotor blade has moved to the left: the turning rotor tilts to the left, not forward.

If you want a rotating rotor, gyroscope or other object to rotate in a particular way, you have to exert the torque 90 degrees before in the rotation.

Answer 2

Image source: Feynman Lectures on Physics book I, chapter 20

The reasoning that Feynman presents is very indirect.

First: the discussion that Feynman offers here is for the case of a fast spinning wheel. When a wheel is spinning fast the gyroscopic effects are significantly larger than the inertia of the non-spinning wheel. For the purpose of simplicity Feynman treats the inertia of the non-spinning wheel as negligable compared to the gyroscopic effects of the fast spinning motion.

So: if the wheel would not be spinning you would need a bit of torque around the x-axis to get the reorientation depicted in fig. 20-2, but as I said, Feynman treats that one as negligable.

Feynman points out the following: the spinning wheel is subjected to rotation around the x-axis. The result of that is a change of the direction of the angular momentum of the spinning wheel. In the picture the length of the vector for the angular momentum is not to scale. Think of the angular momentum vector as a very very long vector. The vector $\Delta L$ represent the change from previous angular momentum to new angular momentum. Think of that vector $\Delta L$ as a very very long vector. (This is why Feynman only considers the corresponding torque, everything else by comparison negligable.)

Feynman then reasons as follows: the torque that corresponds to the vector $\Delta L$ is a torque around the z-axis. So: as you were reorienting the wheel from initial angular momentum to new angular momentum you must have been exerting the forces $F$ and $-F$ which both lie in the xy-plane.

Notice that here Feynman doesn't attempt to explain. He is laying out: if you apply the formulas as presented earlier in the chapter this is the result you get.