Wrong mathematical conclusion from electromagnetism

Question

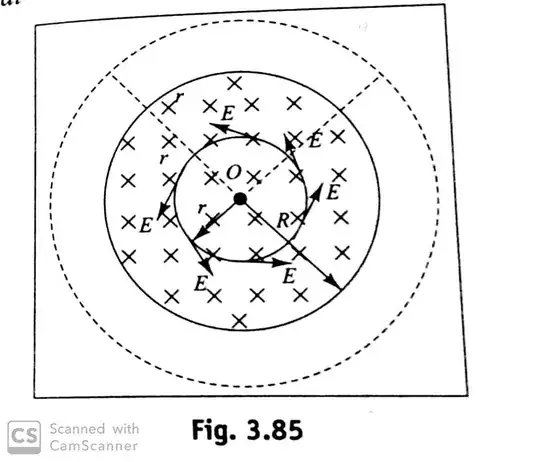
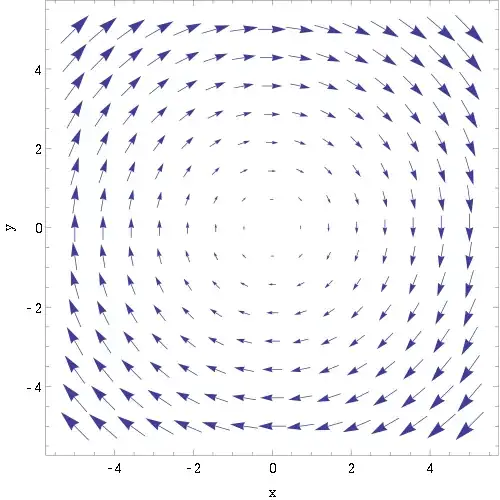
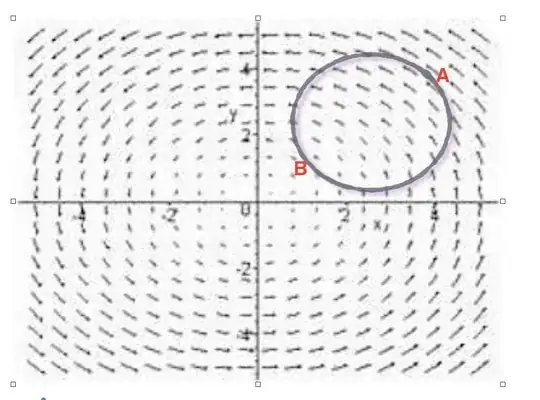
Now suppose a magnetic field is increasing inwards and we keep a loop of radius $r_B$ as shown in the picture below.

$\oint\mathbf E\cdot \text d\mathbf l= \text d\phi/\text dt$, which means $E(2\pi r_B)=(\pi(r_B)²)*(\text dB/\text dt)$(as the electric field is uniform in magnitude around the loop).

The magnitude of the electric field induced should be uniform because of symmetry, as according to my textbook (without any much said reason)

$$\text{For } r<R, E_n(2\pi r)=\pi r^2\,\left|\frac{\text dB}{\text dt}\right|\to E_n=\frac r2\cdot\left|\frac{\text dB}{\text dt}\right|$$

Which means the Electric field at point A is given $E_A=(r_B/2)*(\text dB/\text dt)$

Now if I keep a small loop of radius $r_s$ such that $r_s<r_B$ as shown in the below figure.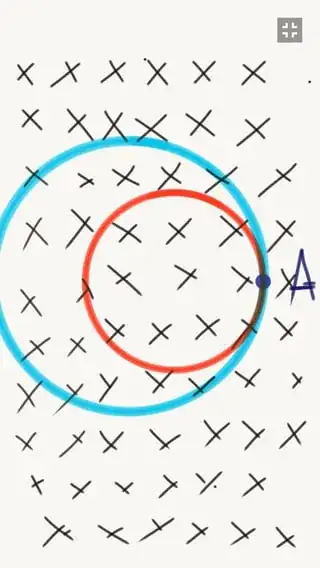

Note small loop is kept after removing large loop means two loops are kept one after another.

Now again applying Maxwell’s equation around loop $\oint\mathbf E\cdot\text d\mathbf l=\text d\phi/\text dt$ and using same method as above we get electric field at A as $E_A=(r_s/2)*(dB/dt)$. Why does the electric field induced depend on loop kept in the field?

From my intuition, I think the electric field at a point induced should be independent of size of loop. So, from the earlier shown equation we see that $$ \frac{r_s}{2}\cdot\frac{\text dB}{\text dt}=\frac{r_B}{2}\cdot\frac{\text dB}{\text dt}$$

so $$r_s=r_B$$ But this is a contradiction to our assumption that $r_s<r_B$.

Please consider explain where I am going wrong. Thank you in advance.

Please explain why and how loop choice affects exactly.Then give priority to explain from mathematical equation.

Answer 1

Now it is questioned that why electric field induced should be uniform.The only answer to this that i know is symmetry.

This actually is the key assumption that leads to your problem.

With the given information we are looking for equations of the form $\nabla \times \vec E = const$. These have solutions like $\vec E = (-y+y_0,x-x_0,0)$.

If you calculate $\oint \vec E \cdot d \vec l$ for a given size circle you will find that it is the same no matter where you center the circle and no matter $x_0$ and $y_0$. However, despite the integral being the same, the value of $\vec E$ is different on different circles. So the function is not unique, but requires the additional specification of some boundary condition. In particular, it requires the specification of the location where $\vec E=0$ which is $(x_0,y_0,z)$.

The assumption that the E field is uniform in magnitude is the assumption that the zero location is at the center of the loop. Therefore, when you move your center and apply the symmetry condition then you are getting a different solution. Each solution is individually valid, but they are not the same solution. That is why you are getting different values for the E-field.

If you calculated the E-field over the entire plane for the first situation, and then drew the second loop and calculated $\oint \vec E \cdot d \vec l$ then you would find that it was also valid, even though it is not uniform. So that single value of the E field is consistent with both the large centered loop and also the smaller and off centered loop, but you cannot use the symmetry rule for both loops simultaneously.

Answer 2

Dale's answer is great for considering the field in your configuration. However, there are some things I want to address, and I want to focus on the diagram you have supplied from your book.

One issue here is that your assumed magnetic field configuration is not physical. A uniform field that covers all space $\mathbf B=B_0\,\hat z$ has an issue, for the current density is $0$: $$\nabla\times\mathbf B=\mu_0\mathbf J=0$$

This is reminiscent of (although not exactly similar to$^*$) the problem of asking what is the electric field for a uniform charge density that fills all of space. You haven't supplied sufficient boundary conditions. So it makes sense that when you try to do certain physics problems that rely on this field you end up with some weird answers.

Dale's answer somewhat fixes this by stating that you need to specify $\mathbf E=0$ at some point, but I suppose this will be somewhat unsatisfying to you since in your setup there isn't any physical reason to pick one point over another for this to be the case. This is why your textbook is only considering a finite circular region of uniform field. Now fields can go to $0$ at infinity, and we have the symmetry we need by making our loop to integrate over concentric with the circular region containing the changing magnetic field. Also note that this now works with Dale's answer, as the point where $\mathbf E=0$ that we need is obviously located at the center of our circular region of magnetic field.

To summarize:

Please explain why and how loop choice affects exactly

You have not supplied sufficient boundary conditions to your system, and you are working with a magnetic field that is not physical. So you are arriving at ambiguous results. To fix this, you need to work with a magnetic field configuration like one shown in your book. Then everything will work out fine (you won't get different fields at the same point in space).

---

$^*$I suppose a more analogous system would be a uniform electric field over all space, so that $\nabla\cdot\mathbf E=\rho/\epsilon_0=0$, and we get no charge density throughout all space. How can no charge anywhere produce an electric field?

Answer 3

The equation $$\oint \mathbf E \cdot d\mathbf l = - \frac{d\phi_B}{dt}$$ comes from the equation $$ \nabla \times \mathbf E = -\frac{\partial \mathbf B}{\partial t}$$ it says that the curl of electric field points in the direction perpendicular to electric field and directly opposite to magnetic field. If we see your situation we can easily infer that the electric field is going to swirl clockwise in the $xy$ plane. So, the picture of the electric field is going to look something like this

(image courtesy: here ) So, you can see that electric vector field is swirling with respect one point (in my picture it is point zero =, only for explanatory purpose). Now let's calculate the circulation by making circle centered at point zero,

in this case I can very well see that $\mathbf E \cdot d\mathbf l$ is constant and equal $E~dl$ therefore (if my circle's radius is $r$) $$ \oint \mathbf E \cdot d\mathbf l = E~2\pi r$$ Now consider this image

you see at point A the electric field arrow points in the same direction as the line element $dl$ of our circle but at point B it points in the opposite direction of $dl$ (we are taking the right hand Cartesian system). Also, notice that the magnitude of $\mathbf E$ at point A is different than at the point B (the density of arrows shows this character). Therefore, in this case we cannot write $$\oint \mathbf E \cdot d\mathbf l = E~2\pi r'$$ And that's the mistake you made when you wrote $E~2\pi r_s$ for your blue loop. For your blue loop $\mathbf E \cdot d\mathbf l$ doesn't equal to $E~2\pi r_s$ as electric field is not constant at the boundaries (both in direction and magnitude it's not constant).

I hope my answer may help you somehow. Queries are welcomed in comments.

Answer 4

May it not answer your question but I want to point that equation from your book is for point inside a loop:

$E_n=\frac{r}{2}|\frac{dB}{dt}|$ for $r<R$ where R is radius of loop,

so you should not use it to calculate electric field at point A because it is on loop $R_A=R_{loop}$.

If you chose 2 loops with the same center point but with different radius that eg.$R_{loop1}<R_{loop2}$ and you take point $B$ that $R_B<R_{loop1}<R_{loop2}$ results of Electric fild in point B form both loops in different size will be the same.

For what is index $n$ in $E_n$ ? It mean tat is E for point "n" or some other meaning?