I am curious about the relationship between energy and information. I have only a beginner's knowledge, having read Shannon's original paper and a little about Landauer's limit which states that the minimum amount of energy required to erase 1 bit of information is about 0.0175 eV at room temperature (about the energy of a single photon in the mid-infrared). I'm aware of Szilard's engine, the concept of physical information, and have looked around this site for a satisfying answer to the question "What is information?" which clearly separates or inextricably intertwines the mathematical concept of information and its necessarily physical storage medium, and haven't found one. This feels related to whether the unit "bit" will ever qualify as an SI unit.
I came up with a thought experiment/toy model to attempt to frame and sharpen this question. The level of detail of the setup can surely expanded or abstracted as necessary, but consists essentially of a light source, a 3d object, and a 2d sensor array.
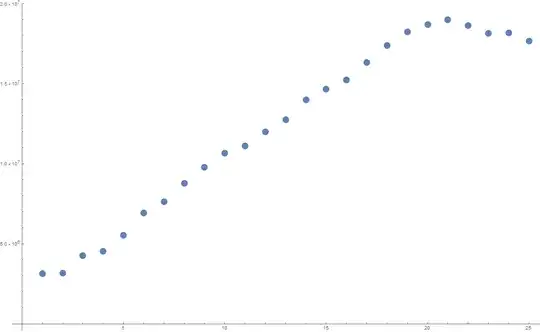
Given a light source (camera flash/light bulb/photon gun) and some object (say, an exotic animal with iridescent scales, a 3d-printed plastic red cube, or a tank of hydrogen gas), if we take a digital photo in a pitch black environment, the sensors (CCD pixels/PMTs) will read out an array of 0's. Using Kolmogorov's definition of information, this is highly compressible and will be a small amount of info. On the other hand, if we turn up the power of a light bulb and make it extremely bright, the image will be 'washed out' and the data will read all 1's, which is also highly compressible. However, somewhere in the middle, there will be an image of the object which isn't very compressible, and so will contain more information. If we vary the brightness continuously, and average over many different objects, we expect a smoothly varying concave function which peaks somewhere in the middle. Normalizing with zero brightness 0 and maximum brightness 1, we might guess the peak occurs at 1/2.
I downloaded a camera app (Manual Camera) on my phone that allows one to manually change the exposure settings (aperture, ISO, & shutter speed), and tested this out by keeping the light constant and changing one of them over 25 gradations and used about 15 different objects. The full dataset is ~500mb (https://www.dropbox.com/s/c4s3egg3x47u340/brightness_v_info.zip?dl=0). Since .jpeg is already a compression algorithm, I take the filesize to be a rough approximation of K-complexity. The resulting plot is attached (x-axis are the 25 brightness settings, y-axis is filesize in bits).
A quick calculation shows that if the shutter speed is $(1/500)s$ and the bulb was 60w, at peak information transfer I used about $.12J$ ($7.49*10^{17} eV$) per $18 Mbit$, or about 41.6 $GeV/bit$ (slightly worse than Landauer's limit).
If we refine to the level of individual photons (i.e. use a 'gun' that shoots one photon of energy $hf$ at a time), I suppose we'd view each photon as a wave which scatters off the object, and then is detected or not with some probability by one of the sensors in the array. Let's assume we shoot $N$ photons of the same frequency. Each object should have its own emission spectrum (colors) which we may or may not be keeping track of with the sensors.
My hope is that in this model, we'll be able to keep track of all the energy and information present. Assuming both are conserved, this might ideally illustrate a bit better their hazy relationship.
Q1: In the mathematical model for one of the outlined physical setups, where should the peak occur on the "info v. brightness" curve for a generic object?
Q2: Is any of the initial energy of the light source (bulb wattage * time, or N*hf) converted into physical information?
Thank you!