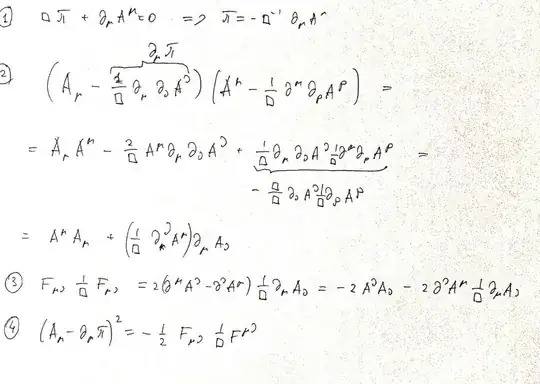This picture is from Schwartz book on QFT on page 131. I cannot understand that:
What does the orange underlined sentences mean?
How is Equation 8.108 derived?
Could anyone kindly make some further explanation on this?
By @Nikita ‘s answer, I think I’ve understand all the rest except this little calculation...
I could get that
$(A_\mu+\partial_\mu \pi)^2=A_\mu A^\mu-A_\mu \frac{2}{\square} \partial_\mu \partial_\nu A^\nu+\frac{1}{\square}\partial_\mu \partial_\nu A^\nu \frac{1}{\square}\partial^\mu \partial_\rho A^\rho$
While
$\frac{1}{\square}\partial_\mu \partial_\nu A^\nu \frac{1}{\square}\partial^\mu \partial_\rho A^\rho =\frac{1}{\square}\partial_\mu \partial_\nu A^\nu \frac{1}{\square}\partial_\rho A^\rho-\frac{\square}{\square}\partial_\nu A^\nu \frac{1}{\square}\partial_\rho A^\rho$
Why does $\frac{1}{\square}\partial_\mu \partial_\nu A^\nu \frac{1}{\square}\partial_\rho A^\rho$ vanish?
How to get $\frac{1}{\square} (\partial^\nu A^\mu)\partial_\mu A_\nu$?