Van Der Waal's equation leads to a cubic equation in v of the form
$$Pv^3-(bP+RT)v^2+av-ab=0$$
This equation has 3 roots for $T<T_C$ and one root for $T>T_C$ 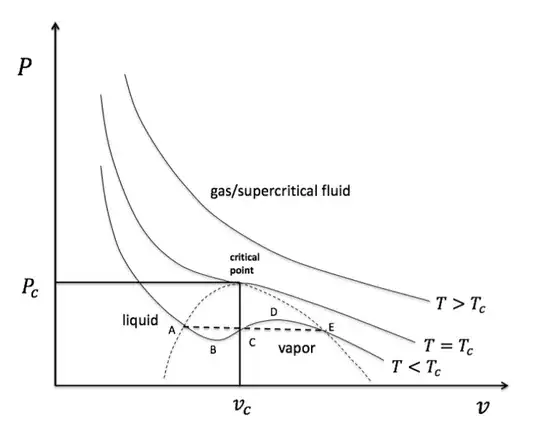
I understand why region ABCDE is physically unrealized (for path ABC pressure goes down while volume decreases, and for path CDE, pressure goes up and volume goes up) and experimentally we observe a straight line AE (dashed). Maxwell's construction helps to correct this part of Van Der Waal's equation by arguing equal area in region ABC and CDE. As a result we get the stragiht line AE (dashed).
I understand that Gibbs energy is not minimized and hence it's not an equilibrium state. I wanted to understand this notion from a bifurcation point of view. So, my questions are
1) What type of bifurcation it goes through? (I am guessing some sort of pitchfork bifurcation?)
2) How can the path ABCDE be argued to be non physical from a non-linear dynamics point of view? Thanks