3

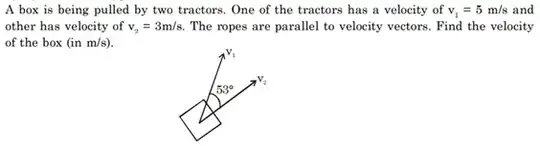
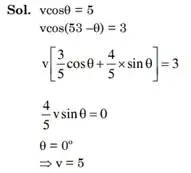Consider the following two situations.

Case I

enter image description here

I am able to solve this question. The answer to this question is = 5 m/s. I have attached the solution in the end.

This is not the doubt. Kindly read further to understand the theoretical doubt.

Case II

Now, in Case I, suppose we replace the velocities by two Forces F1=5N and F2=3N, applied on the body in the same directions as in Case I and we are supposed to calculate the net force on the body, and this modified situation, we call Case II.

Now, in Case II, we can apply the formula for net force given by the Parallelogram Law of Vectors as shown below and that gives the right answer in Case II. But, interestingly, when the same knowledge of Parallelogram Law is applied in Case I, it doesn't give the right answer. According to my textbook applying Parallelogram Law in Case I, like Case II, is wrong. I do not understand the reason behind it.

Both, Force and Velocity are vectors and Parallelogram Law of Vectors, as I understand, should be applicable for all the vectors, so why it is the case that Parallelogram Law of Vector Addition gives the right answer in Case II, but NOT in Case I.

Why are we treating the Force Vector and Velocity Vector differently?

I would appreciate both - Mathematical and Intuitive Understanding.

enter image description here

The solution to Case I. Let's say the net velocity is V then the components of this velocity along V1 and V2 should be equal to V1 and V2 itself, due to string conservation and hence following is the solution. "Theta" is the angle net velocity makes with V1 (Let's say).

enter image description here

Devansh Mittal
  • 2,577

4 Answers4

1

The following are the ideas to understand the difference between Force and Velocity Vectors.

  1. We cannot apply Parallelogram Law in the above case to find the net velocity of the object.

  2. Force vector and velocity vectors are not the same. An object may experience two forces at the same time but an object may not have two velocities at the same time. The velocity of an object can only have only one value, in one direction. One may point out an example showing an object possessing two velocities at the same time, as @Trula in another response pointed out, but that could be the case only in Relative Velocity when the object is moving on another moving platform. That is not the case in the given question.

  3. V1 and V2 are NOT the two non-rectangular components of the net velocity vector. It is not given in the question, so it would be wrong to assume so, and hence we cannot apply Parallelogram Law on V1 and V2 to find out the net velocity of the object.

  4. The component of net velocity in the direction of V1 will be equal to V1, by string conservation. And, the component of net velocity in the direction of V2 will be equal to V2, by the string conservation. We use this knowledge to solve the question.

Devansh Mittal
  • 2,577
1

Let us go back to the original question: an object is attached by ropes to two tractors, moving at constant velocities". I would first like to note that of course velocity is a vector quantity, and so it can be decomposed into orthogonal, or non-orthogonal, components exactly as you wish. That is not the problem here though, and making a vector sum of the tractor's velocities does not tell us anything useful. What we have instead is a (concealed) problem in dynamics.

The two ropes exert forces on the object. In this case they will be tension forces. If we know these forces then we can sum them together using the parallelogram rule, find the resultant force, and then use Newton's second law to find the object's acceleration. The problem does not give the forces though; it gives the velocities of the tractors, which makes analysis of the problem more subtle.

Tractor 1 is moving away from the object at higher speed than tractor 2 (5 m/s compared with 3 m/s), so that its rope will be pulled taut. However, the rope connecting tractor 2 to the object will be slack, and so will not exert any force. After some transient acceleration, the object will thus acquire the same velocity of tractor 2, a situation we are familiar with if we have ever towed another vehicle. Tractor 1 simply does not participate, at least until it drops so far behind the other vehicles that its rope tautens, and it starts to drag back on them.

Clara Díaz Sanchez
  • 2,415
  • 1
  • 10
  • 21
0

The velocities add exactly like the forces, her to about 7,21m/s not to 5. the solution you give is wrong. Do you really believe , that the net velocity is exactly the size and direction of v1? The equation which gives you sin(theta)=0 is wrong. may be you just add the two vectors graphical to see it?

trula
  • 6,940
-1

Both, Force and Velocity are vectors and Parallelogram Law of Vectors, as I understand, should be applicable for all the vectors

Yes you are correct both force and velocity are vectors and in both the cases parallelogram law of vector addition is applicable,so what is the catch here?

Why are we treating the Force Vector and Velocity Vector differently?

Now, yes adding two forces vectorially is correct but have you ever thought that velocity and force vectors are non interchangeable?? If you had replaced velocity vectors with force that would have been totally wrong,but why? A velocity vector need not be in the direction of the force vector.

Let me give you an example to make this intuitive, If we throw a ball upwards the acceleration due to gravity $g$ always acts downwards hence the force due to gravity is acting downwards,but do you realise? The force vector is towards downward direction and the velocity vector is in the upward direction. Both these vectors are acting in completely different directions and so they are not interchangeable

So yes you are correct that force is a vector,but if you had assumed the correct direction of force vectors and added them then you would have arrived to the correct solution in case 2 Hope this helped

Rishab
  • 68