I'm having a hard time with understanding how to model the rotational kinetic energy of rigid bodies. I will appreciate any good suggestion about resources such as books or videos regarding topics like adding angular velocity vectors (with inclined axis), and how to calculate Inertia Moments and Inertia Tensors. These are some exemples of the systems I will try to model:
Any suggestions or advice will be really helpful. Thanks in advance.
Not a book recommendation, but a quick overview of the process in hopes to fill some holes in your understanding, or to spark the correct questions to ask.
Like you mention in your post, you need to know the the translational velocity of each body center of mass $\boldsymbol{v}_i$, the rotational velocity $\boldsymbol{\omega}_i$ of each body, and the mass moment of inertia tensor $\mathbf{I}_i$ of each body at each center of mass. Then you can evaluate
$$ \mathrm{KE} = \sum_i \tfrac{1}{2} \boldsymbol{v}_i \cdot (m_i \boldsymbol{v}_i) + \sum_i \tfrac{1}{2} \boldsymbol{\omega}_i \cdot (\mathbf{I}_i \boldsymbol{\omega}_i) $$
where $\cdot$ is the vector dot product.
This is complex task becauses there are a lot of details to consider. Nevertheless once you know what you know it is rather straightforward. This process works for all systems that can be viewed as a tree structure with one root body connected to the ground, and then one or more children bodies each connected with a 1-DOF joint to its parent body. So each body is a attached to end "top" of only one joint.
Position Kinematics
Recursively starting from the root object you calculate the position and orientation of the top of each joint $\boldsymbol{d}_i$ as well as the position of the center of mass $\boldsymbol{r}_i$ for the body attached to the joint. The orientation is described using a 3×3 rotation matrix $\mathbf{E}_i$. Each is a function of the joint degree of freedom $q_i$, which is either a distance or an angle value depending on the type of joint.
$$ \begin{aligned} \boldsymbol{d}_i & = \boldsymbol{d}_{i-1} + \mathbf{E}_{i-1} \,\left(\mathrm{base}_i+ \mathrm{pos}(q_i) \right)\\ \mathbf{E}_i & = \mathbf{E}_{i-1} \,\mathrm{ori}(q_i) \\ \boldsymbol{r}_i & = \boldsymbol{d}_i + \mathbf{E}_i \mathrm{cg}_i\\ \hline \boldsymbol{d}_0 & = \boldsymbol{0} \\ \mathbf{E}_0 &= \mathbf{1}_{3×3} \end{aligned} $$
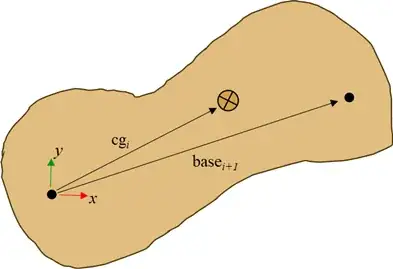
Note that $\mathrm{base}_i$ is the location of the "base" of each joint in local coordinates of the previous body. For example a link of length $\ell$ with the next body connected along the x-axis then $\mathrm{base}_i = \pmatrix{\ell \\ 0 \\ 0}$. Similarly $\mathrm{cg}_i$ is the location of the center of mass. See below for a diagram of this
Some example joints is described below:
$$ \begin{array}{r|c|c|c|c} \text{type} & q_i & \mathrm{pos}(q_i) & \mathrm{ori}(q_i) & \text{axis}_i \\ \hline \text{slider along }\hat{i} & x_i & \pmatrix{x_i \\ 0 \\ 0} & \pmatrix{1&0&0 \\ 0&1&0 \\ 0&0&1} & \pmatrix{1\\0\\0}\\ \text{rotate about }\hat{k} & \theta_i & \pmatrix{0\\0\\0} & \pmatrix{\cos \theta_i & -\sin\theta_i & 0 \\ \sin\theta_i & \cos\theta_i & 0 \\ 0&0&1 } & \pmatrix{0\\0\\1} \end{array} $$
Velocity Kinematics
By direct differentiation of the position kinematics, the velocity kinematics are also found recursively. The velocity of the "top" of the joint is $\dot{\boldsymbol{d}}_i$ while the velocity of the body center of mass is $\boldsymbol{v}_i = \dot{\boldsymbol{r}}_i$
$$ \begin{aligned} \dot{\boldsymbol{d}}_i & = \begin{cases} \dot{\boldsymbol{d}}_{i-1} + \boldsymbol{\omega}_{i-1} \times \left( \boldsymbol{d}_i - \boldsymbol{d}_{i-1} \right) + \mathbf{E}_{i-1}( \mathrm{axis}_i \, \dot{q}_i) & \text{slider} \\ \dot{\boldsymbol{d}}_{i-1} + \boldsymbol{\omega}_{i-1} \times \left( \boldsymbol{d}_i - \boldsymbol{d}_{i-1} \right) & \text{rotate} \end{cases} \\ \boldsymbol{v}_i & = \dot{\boldsymbol{d}}_i + \boldsymbol{\omega}_i \times ( \boldsymbol{r}_i - \boldsymbol{d}_i )\\ \boldsymbol{\omega}_i & = \begin{cases} \boldsymbol{\omega}_{i-1} & \text{slider} \\ \boldsymbol{\omega}_{i-1} + \mathbf{E}_{i-1} (\mathrm{axis}_i\,\dot{q}_i) & \text{rotate} \end{cases} \\ \hline \dot{\boldsymbol{d}}_0 & = \boldsymbol{0} \\ \boldsymbol{\omega}_0 & = \boldsymbol{0} \end{aligned}$$
where $\times$ is the vector cross product.
This is slightly more straightforward as it only involves transforming the body aligned mass matrix $\mathbf{I}_{\rm body}$ into the world coordinate system using the body rotation matrix $\mathbf{E}_i$
$$ \mathbf{I}_i = \mathbf{E}_i \, \mathbf{I}_{\rm body} \, \mathbf{E}_i^\intercal $$
where ${}^\intercal$ is the matrix transpose operator.
