Reason for Symmetry of stress tensors

Question

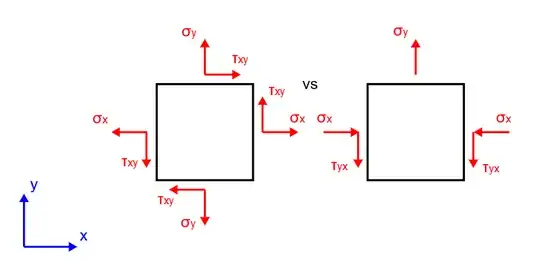
just as all other engineering students, I was taught in my mechanics lectures that stress tensors are always symmetrical. Back in the day I just accepted that fact, but now after some time, I wonder about the actual reason behind that. Consider the exemplary 2D stress states below: Both are capable of fulfilling equlibrium of forces and momentums and are plausbile on a macroscopic scale. Yet on an infinitesimal scale, as we all have learned, only the one on the left hand side can occur. Could anyone explain to me why that is? (sadly I'm no mathematician, so I'd be glad for an "understandable" explanantion ;)

Answer 1

The problem with the right hand diagram is that it doesn't scale properly.

Suppose this stress field was uniform over a finite sized region. Now take a rectangular element of size $\Delta x$ by $\Delta y$. You now have a direct force $\sigma_y \Delta x$ balanced by the shear forces $2 \tau_{yx} \Delta y$ and you can't eliminate $\Delta x$ and $\Delta y$ because they are both arbitrary.

In the left hand diagram, the forces balance for any shape of rectangle, not just a square.

Of course this simple argument only shows that your "wrong answer" is wrong, not the that "right answer" is the only right answer. A more general idea is to consider rotating the small element through an arbitrary angle, and considering that the forces on the edges must be. If you remember what you learned about principal stresses, you can choose an orientation for the element where all the shear stresses are zero, for example.