Why torque is defined to have a direction as the axis of rotation?

Question

Torque is generally defined as the "twisting force". Let's imagine that I have a rod of length $L$ pivoted at it's center. Now, let's assume that the shorter angle between the tail of the force vector and the vector joining the end (the end on which the force is applied) to the center (vector points from the center to the end). 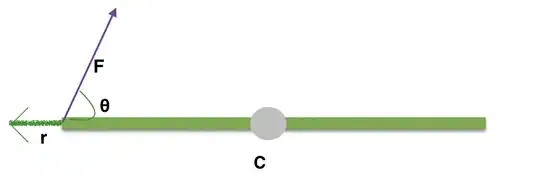Now, the force which will cause the rotation is the vertical component of $\mathbf{F}$ and the horizontal component will have no result because the rod is pivoted. So, the magnitude of the force causing the rotation is $F \sin \theta$ and from the definition of the "twisting force" (experiments shown that force and distance both matter in making a rotation of a pivoted body) $$ \tau = r~F \sin\theta $$ $$ \tau = \frac{L}{2} ~F \sin \theta$$ Although it looks like the magnitude of the cross product but I don't see any reason in defining the torque in above case as $$ \vec{\tau} = \mathbf{r} \times \mathbf{F}$$ $$ \vec{\tau} = - \frac{L}{2} ~ F\sin\theta \hat n$$ where $\hat n$ is the vector coming out of the plane of the rotation. Why torque was given a direction as the axis of the rotation? What is the use of defining the torque as a vector when it's the component of the force that decides the direction of rotation?

score 1 · Answer 1 · answered Feb 02 '20 at 18:40

The definition of torque emanates from the very definition of angular momentum which is: $$\boldsymbol {\ell} = \mathbf r \times \mathbf p$$

And

$$\boldsymbol {\tau} = \frac {d \boldsymbol {\ell}}{dt}$$

Therefore

$$\boldsymbol {\tau} = \mathbf r \times \mathbf F$$

Now this means that we should question the very definition of angular momentum.

So why do we define angular momentum that way?

The following is what I think:

It gives us a nice conserved quantity. Suppose if it were defined as a vector in the direction of velocity of the rotating particle then the direction would be time dependent and hence it wouldn't be a rotational constant of motion.
It can be added vectorially and the prediction and the information that we get from this net angular momentum vector matches reality. Same is true for torque.

score 1 · Answer 2 · answered Feb 02 '20 at 18:57

Well there are obvious mathematical considerations to opt for the widespread usage of cross products and the same applies here too.
Firstly ,why do we need a direction for a vector and that too perpendicular to the plane ?Torque is the product of perpendicular component of force and radial distance magnitude wise , two quantities multiplied can be thought of as areas and that brings you to cross product ,area of parallelogram formed by vectors is magnitude of cross product ,that gives you the perpendicular component bit too.
Now in your setup I assume you are comfortable with the exercise that you can add the torque algebraically to get net torque ,and you also know that vector magnitudes can be added algebraically when they are collinear.Since the forces you apply and radius vectors are in same planes always ,the mobile screen here ,therefore we can represent the magnitudes as vectors pointing out and in the screen ,that way they can be added up algebraically as we already know.The direction is the axis of rotation in this case.This property is also satisfied by our cross product ,giving us two directions with opposite signs for the two kinds of spins for the rod.
These were for the intuitive explanation, this definition of torque acts more like a vector when you are applying forces on a pivoted sphere free to spin in any direction ,then you can work out mathematically that with the same vector-like treatment we can find the net torque due to all forces and it is not even necessary for the individual torques to be coplanar ,but the vector sum of all will surely give the net torque.

score 1 · Answer 3 · answered Feb 02 '20 at 18:58

To my understanding representing torque in the form of a vector is something of a fluke.

In space with 2 spatial dimensions torque is a scalar, and in a space with 4 spatial dimensions (and higher) there is no way to represent torque in the form of a single vector. You have to represent the plane of that torque, and defining a plane requires 2 vectors.

But in a space with 3 spatial dimensions every plane has one and only one vector that is perpendicular to that plane. So in a space with 3 spatial dimensions it so happens that you can use that property for a shorthand notation. Instead of specifying the plane you specify the vector perpendicular to it.

score 1 · Answer 4 · edited Feb 02 '20 at 19:27

From a practical standpoint, let's say that I am standing in front of your rotating rod and I say that it is rotating clockwise. If you are standing behind your rotating rod, you will say that it is rotating counterclockwise. Both of us are correct, but since we are in different reference frames, we will not agree.

This disagreement is resolved with a right-hand rule. I let the fingers of my right hand twist in the direction that the rod is rotating, and I find that my thumb points "into" your drawing on the screen. If I define the torque vector by this rule, then I say that the torque vector points into the screen. When you use the same rule while standing behind the rotating rod, you find that when you let the fingers of your right hand twist in the direction of the rotating rod, your thumb also points into the screen, and thus, the torque vector points into the screen. This means that we will both agree on the direction of the torque vector, despite our different reference frames.

score 0 · Answer 5 · answered Feb 02 '20 at 19:02

Why torque was given a direction as the axis of the rotation? What is the use of defining the torque as a vector when it's the component of the force that decides the direction of rotation?

A net force applied to any extended object (as opposed to a point mass) can result in translation, rotation, or both. Translation is associated with linear acceleration. Rotation is associated with angular acceleration.

Linear acceleration is a vector with magnitude and direction associated with the component of net force in the direction of displacement.

Angular acceleration is a vector associated with the rotation of the object about some point or axis. How shall we describe such a vector?

Since we are dealing with rotation about some point or axis, it is logical to associate the magnitude of such a vector with the degree of rotation about that point or axis.

Since reversing the direction of the applied force changes the direction of rotation (clockwise to counter-clockwise, or vice versa), it seems further logical to adopt a convention for the direction of the vector into or out of the plane depending on the direction of rotation.

The vector so assigned to rotation about a point or axis is readily adapted to the combined effects of multiple torques or moments. Summing the torques or moments about a point or axis results in algebraically summing the torque vectors. Thus a clockwise torque about an axis reduces the magnitude of the net torque about the axis due to a counter-clockwise torque or moment. It may even change the direction of the net torque from into the plane to out of the plane, and vice versa.

Perhaps you can show us a better description of a vector to reflect torque?

Hope this helps.

Why torque is defined to have a direction as the axis of rotation?

5 Answers5