What actually is conduction band?I have just started learning semiconductors and this is the very first concept I am troubled with.Is this continuous energy level of all the free electrons or something else?If they are, then is forbidden energy gap equal to ionisation energy?As ionisation energy is the amount of energy to release the outermost electrons which I suppose is the same as forbidden energy gap?
2 Answers
is forbidden energy gap equal to ionisation energy?
In solids, generally in ones with well defined spatial structure as in crystals, the valence electrons can hop from one atom to the neighbouring atom. In this sense the electrons do not belong to any particular atom, they are delocalised. Thus ionisation energy doesn’t make sense in this context. In fact it is defined only for isolated atoms.
Now the gap exists due to the fact that quantum mechanically, the electron can exist only in discrete energy states. And the gap is just the gap between two allowed states, highest of core and lowest of valence.
That explains the gap. But what about the continuum? Individual atoms have discrete energy states. But when two atoms come close to each other they affect each other to split energy states. This can be understood by the following cartoon: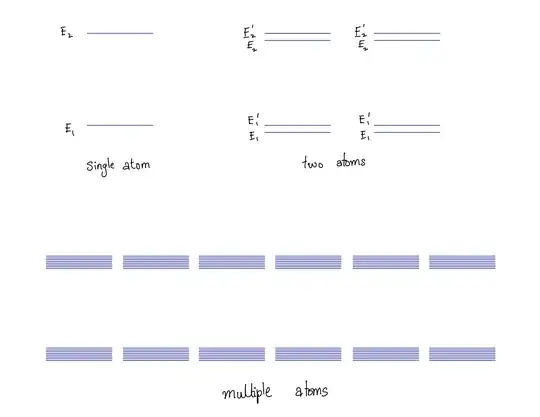
Obviously, the cartoon is an oversimplification of the actual physics but in essence this is what is causing the band (continuum of energy states) to appear. If the action of the neighbouring atom on the electron is less than that due to the current atom, the splitting of energy levels is less than the gap between the states. However if the neighbouring atom’s influence is comparable with that of the current atom, the splitting will be of the order of the gap. In this case, the two bands overlap. This is what happens in metals.
- 9,511
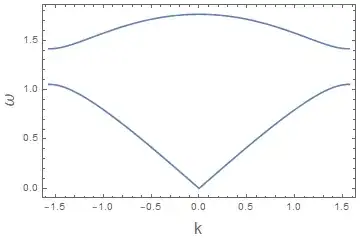
This is the way I like to think about it. You have probably encountered dispersion relations already, which tell you the frequency for a particular wavelength. Here's the dispersion for phonons (vibrations in crystals):
In quantum mechanics frequency and wavelength are related to energy and momentum respectively by $E=\hbar\omega$ and $p=\hbar k$. Each material has its own dispersion relation and this dispersion places constraints on the allowed energies. A free particle has dispersion $E=\hbar^2 k^2/2m$ so any energy is possible but take for example the infinite square well. There the potential forces the energies to only take on discrete values. To go back to the phonon dispersion, let's break up the dispersion so it only takes on discrete values of $k$ to make it easier to visiualize.
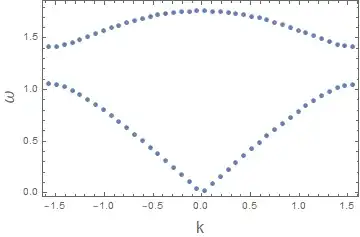
Now imagine you turn the image $90^\circ$ clockwise and let all the points fall down. If you now count how many points fell onto a particular energy you roughly see how many states are available for that energy level. This looks something like this:
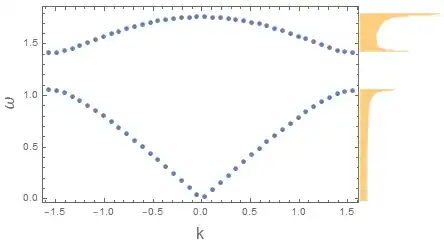
For energy bands we are only interested in whether or not an energy has any available states. To get the energy band you extend the yellow graph so that it reaches all the way if has at least one state state. You basically stretch the yellow graph until it is a rectangle. For some energies there are zero states so even after this stretching it is still empty. This is a band gap.
In quantum mechanics each state can only be occupied by one particle (for fermions, which include electrons) so usually the states are filled from the bottom up. Energy and momentum conservation still apply so to excite an electron from the lower to the upper band it has to absorb an energy that is at least as large as the band gap.
Edit in response to @garyp: I used energy dispersion a bit loosely. Phonons do have a dispersion and are a nice example but this 'band gap' is different from that in semiconductors. Phonons are not quantum objects so the frequency of a phonon is not its energy. To get electronic dispersion relationships like for semiconductors you would have to solve the Schrödinger equation and then the resulting dispersion will give you the energy.
- 19,613