0

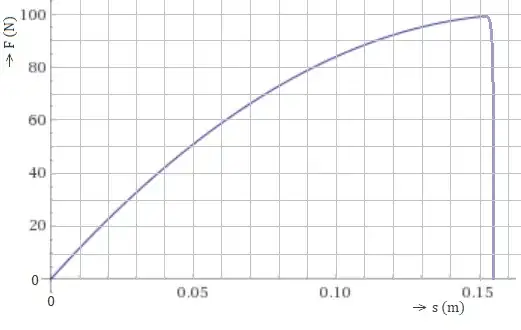
I'm making a set of exercises as part of a college project, aimed at 4th year middle school physics. In an exercise on spring constants, i used balloon inflation as a new example, i made the following graph:

graph of force vs balloon radius

where s denotes radius (perfect sphere). The sharp slope at the end is caused by the balloon exploding, hence no force remains. I'm unsure whether this graph is realistic however. I think the slope should actually increase, as the force has to be spread out over 2 directions, instead of 1 in a spring (straight diagonal line). So on that basis, this graph isn't realistic, right?

I don't want to make another graph however. So i was wondering whether I could justify it if i add that the rubber of the balloon gets weaker/thinner (or: the spring constant of the rubber decreases) as it stretches. Or would the graph still make no sense then?

Edit: my main question: could this graph be realistic for a balloon being inflated. Here F is the force required by the person inflating the balloon, or more precisely the total force distributed over the balloon. Or should i really replace it with a quadratic shape (so graph^(-1))?

Bowie N.
  • 3

1 Answers1

1

The situation you describe is far more complex than it may appear. Let me break it down into three parts.

(1) On spring constants: The assumption that materials behave like linear springs is called the linear elasticity assumption. This is valid for very small strains, certainly not to the type of failure strain you are considering.

To understand this better, consider a typical potential between two atoms, say a Lennard-Jones potential. At any point (i.e. any spacing), the derivative(slope)of this curve gives the force at that point. Look at the bottom or the minima of the curve. Upto very small deviations on either side, you can assume the slope is constant. Only within these very small deviations can you assume a linear spring.

Depending on the type of material, the exact equation for this curve, or the potential, will vary. In most of them, the slope would reduce as you move away from the minima. This means that the force for an additional stretch keeps on reducing.

(2) On the reduction in thickness: The volume is not necessarily constant as you deform the balloon. Volume constancy is a necessary condition only in plastic deformation, i.e. where you impart a permanent deformation. So the balloon may think, but not necessarily in the ratio you expect it to. You cannot make any estimate or justification without knowing the specific material constant for the balloon material. This constant is called the Poisson ratio.

(3) On expansion in two dimensions: Why two? It is expanding in 3-d space. If you assume that it remains perfectly spherical, you can consider that any point on the balloon surface would satisfy the equation of a sphere, i.e.

$x^2 + y^2 + z^2 = r^2$

You can now assume that $x=y=z$ and reduce the equation to $x^2=r^2/3$. Once you have the change in position x with respect to radius change, you directly can apply the spring equation (for very small strains of course).

AppliedAcademic
  • 554