Measuring the solar system's speed through ether with the help of an eclipse

Question

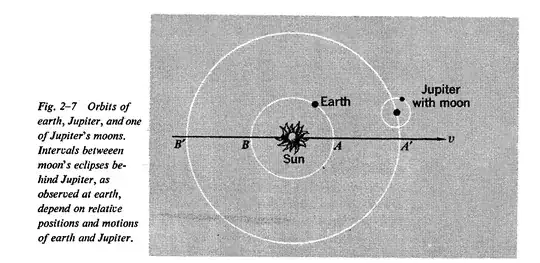
In A.P. French's Special Relativity, the author said,

Jupiter has a period of $12$ terrestrial years, and so in half a terrestrial year, while the earth moves from $A$ to $B$ (Fig. $2$-$7$), Jupiter does not travel very far in its orbit. Thus by observing the apparent times of eclipses with the earth successively at $A$ and at $B$, we can infer the time taken for light to travel a distance equal to the diameter of the earth's orbit. This was Roemer's discovery, in fact. But if this time is measured when Jupiter is first at $A'$, and then, $6$ years or so later, at $B'$, we can hope to discover whether the whole solar system is moving through the luminiferous ether with some speed $v$.

For, if the diameter of the earth's orbit is $l$, we would expect to have $$t_{1}=\frac{l}{c+v}~~~~~~~~~~~~~~~~t_{2}=\frac{l}{c-v}$$ and hence a time difference $\Delta t$ given by $$\Delta t=t_2-t_1\approx\frac{2lv}{c^2}=\frac{2v}{c}t_0$$ where $t_o = 16$ min approximately.

The text is talking about measuring the duration of the eclipses when Jupiter is first at $A'$ ($\Delta t_{1}$, say), and then at $B'$ ($\Delta t_{2}$). But On the other hand $t_1$ is obviously the time taken by light to travel from the sun to Earth when Jupiter is at $A'$, and $t_2$ is the time taken by light to travel from the sun to Earth when Jupiter is at $B'$.

After seeing the equations, the text seems rather ambiguous: The text is talking about "measuring" times, yet there is no way we can measure $t_1$ and $t_2$.

How is $t_{1}$ (or $t_2$) actually related to $\Delta t_1$ ($\Delta t_2$)? Am I misinterpreting $t_1$ and $t_2$?

Or, simply put, shouldn't $t_1$ be $AA'/({c-v})$ and $t_2$ be $BB'/({c+v})$?

Answer 1

1. In this answer, Adam Zalcman describes how Roemer determined the speed of light using the orbit of one of Jupiter's moon called Io. Go through his answer (with the help of this section from Wikipedia, if needed). More specifically, I want you to understand how he obtained equation $(1)$ because it's a prerequisite to understanding my answer. $$\Delta t=t_1-t_0-nT=\frac{d_{EJ}(t_1)-d_{EJ}(t_2)}{c} \tag{1}$$
2. Consider the picture you have posted in the question. Let's assume that Earth, Jupiter, and Io orbit in the anti-clockwise direction as seen from above. I'm going to run down the events as Earth travels from $A$ to $B$ while Jupiter approximately stays put at $A'$ due to its 12-terrestrial-year large period. We make successive Earth-based observations of Io's periodical emersions, starting from $t=t_0$ (observed the $1^{\text{st}}$ emersion) when Earth is at $A$, till $t=t_1$ (observed the $n^{\text{th}}$ emersion) when Earth reaches $B$. $$\text{When did the $1^{\text{st}}$ emersion actually take place? : }\tau_1$$ $$\tau_1=t_0-\underbrace{\frac{d_{EJ}(t_0)}{c+v}}_{\text{Time taken for light to travel from Jupiter to Earth}}=t_0-\frac{AA'}{c+v} \tag{2}$$ $$\text{When did the n$^{\text{th}}$ emersion actually take place? : }\tau_n=t_1-\frac{d_{EJ}(t_1)}{c+v}=t_1-\frac{BA'}{c+v} \tag{3}$$ $$\tau_n -\tau_1 = nT \Rightarrow t_1-t_0-nT=\frac{BA'-AA'}{c+v}=\frac{l}{c+v} \tag{4}$$ $$t_1^{\text{A.P. French}}\stackrel{\text{Definition}}\equiv t_1-t_0-nT \;\Biggr| \;t_1^{\text{A.P. French}}=\frac{l}{c+v} \tag{5}$$ Approximately half a terrestrial year is spent to determine $t_1^{\text{A.P. French}}$ : $t_1$, $t_0$, $n$, and $T$ (orbital period of Io: $T \approx 42.5 hr$) are known from observations. Now, we wait six terrestrial years for Jupiter to reach $B'$ and then repeat the same experimental observations to determine $t_2^{\text{A.P. French}}$. This time, we get: $$t_2^{\text{A.P. French}}=\frac{l}{c-v} \tag{6}$$ If our solar system were truly moving with respect to the ether with velocity $v$ along the direction $AA'$, then equations $(5)$ and $(6)$ predict that $t_1^{\text{A.P. French}} \neq t_2^{\text{A.P. French}}$.

Thus by observing the apparent times of eclipses with the earth successively at A and at B, we can infer the time taken for light to travel a distance equal to the diameter of the earth's orbit.

The more I read the above statement, quoted from the textbook, the more suspicious I become of my reasoning. I can't understand the above statement clearly. All the same, the reasoning I've stated above is the only way I can make sense of what has been said in the textbook.

Don't hesitate to ask for clarifications in the comments.

Answer 2

Careful with the geometry, yes the Earth goes from A' to B' whilst Jupiter moves very little across the sky. So the distance you need for t2 is not BB' but A'B' which is the diameter of the Earth's orbit (2AU)

Your choice of BB' for t2 is an error because Jupiter is not at B' when the Earth is at A'.

So, yes t1 is the duration for the eclipse observed at A closest to Jupiter and t2 the duration of the eclipse observed at t2 distance B'A'. Remember Jupiter is assumed stationary during this time as it takes 6years to get to B'.

The difference t2 -t1 gives the time it takes for light to cover the distance AB - the Earth's diameter.

Next step is to think about the relative velocity of the Earth v, wrt Jupiter (stationary), and the velocity of light c, towards and away from Jupiter.

Heading towards Jupiter Roemer found t1 was smaller than expected (at A) and t2 larger than expected when furthest away (at B).

The relative velocity for the smaller than expected time t1 (approaching Jupiter) is c-v and that for t2 ( Earth moving away) is c - v.

t1 = A'A/(c+v). and t2 = A'B/(c-v)

Then take it from there so, delta t = t2 -t1 =..., etc. Remember, the difference in distances, A'B - A'A is the diameter of the Earth's orbit. AP French use the letter l for the diameter (AB).