Strain energy stored in an infinitely thick-walled spherical pressure vessel

Question

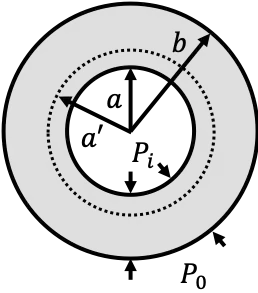
I'm not sure how to approach the following problem. Consider an infinitely thick walled spherical pressure vessel with undeformed internal radius $a$ and outer radius $b\rightarrow\infty$ made of a linear elastic material where, in its undeformed state, the pressure inside the vessel $P_i$ is equal to the outside pressure $P_o$, see figure.

If $P_i$ is increased the inner wall is deformed to $a'$. How do I calculate $a'$ as a function of $P_i$ for a linear elastic material?

I should then be able to integrate $P(a')dV$ to find the work done, which should be equal to the strain energy stored in the vessel. Is this correct?

Update:

I've made some progress. Following this answer: Stress in a thick-walled pressure vessel the displacement, $u$, of the material in the sphere can be written

$u(r)=\frac{P_i-P_o}{4G}\frac{a^3}{r^3}r$,

where G is the shear modulus of the material. So if $a'=u|_a+a$,

$a'=a(\frac{P_i}{4G}+1)$.

Or, in a more convenient form,

$P_i=4G(\lambda-1)$

where $\lambda = a'/a$.

I'm still not sure how to find the strain energy stored in the sphere however..

Answer 1

Following from Chet Millers answer, an alternate solution to the strain energy can be found if instead the pressure inside the vessel is slowly increased. The work done, $U_w$, in deforming the inner wall of the pressure vessel from $a$ to $a'$ will be equal to the strain energy stored if there are no dissipation processes.

First the internal pressure, $P_a$, can be found as a function of $a'$ in the following way. From Chet's solution the displacement of the inner wall can be written $$u=\frac{P_a-P_{\infty}}{4G}a.$$ We'll want to integrate over $a'$, so $P_a$ can be written in a more convenient form given $a'=a+u$, $$P_a = 4G\left(\frac{a'}{a}-1\right)+P_{\infty}.$$ $U_w$ can now be found by integrating the $P_a$ over the change in volume: $$U_w=\int_{V}^{V'} P dV = 4 \pi \int_{a}^{a'}P_a(a')^2da'$$ Setting $P_{\infty}=0$ (as $P_{\infty}$ will result in some arbitrary constant time the volume) and carrying out the integral the strain energy, $U$, is found to be $$U=U_w=16 \pi G a^3 \left(\frac{\lambda^4}{4}-\frac{\lambda^3}{3}+\frac{1}{12}\right),$$ where the stretch $\lambda = a'/a$.

The difference (I think) between this solution and Chet Miller's is that the pressure is slowly increased rather than added instantly.

Answer 2

In spherical coordinates, the equation of continuity for an incompressible material experiencing this deformation is $$\frac{1}{r^2}\frac{d(ur^2)}{dr}=0$$The strains are $$\epsilon_r=\frac{du}{dr}$$ $$\epsilon_{\theta}=\frac{u}{r}$$ $$\epsilon_{\phi}=\frac{u}{r}$$

From the continuity equation, it follows that $$u=\frac{a^2}{r^2}u_a\tag{1}$$So the strains are:$$\epsilon_r=-2\frac{u_aa^2}{r^3}\tag{2a}$$$$\epsilon_{\theta}=\epsilon_{\phi}=\frac{u_aa^2}{r^3}\tag{2b}$$ The stresses are then given by: $$\sigma_r=-p+2G\epsilon_r=-p-4G\frac{u_aa^2}{r^3}\tag{3a}$$ $$\sigma_{\theta}=\sigma_{\phi}=-p+2G\frac{u_aa^2}{r^3}\tag{3b}$$ where p(r) is the isotropic portion of the stress tensor (to be determined).

For the present spherically symmetric problem, the radial component of the stress-equilibrium equation reads: $$\frac{1}{r^2}\frac{d(r^2\sigma_r)}{dr}-\frac{(\sigma_{\theta}+\sigma_{\phi})}{r}=0\tag{4}$$ If we substitute Eqns. 3 into Eqn. 4, we obtain: $$\frac{dp}{dr}=0$$or$$p=const.$$ We can obtain the value of the constant by evaluating the radial stress at r = a: $$-P_a=-p+\frac{4Gu_a}{a}$$where $P_a$ is the pressure inside the cavity. This gives $$p=P_a-\frac{4Gu_a}{a}\tag{5}$$At large values of r, the radial stress approaches $-P_{\infty}$. So we also have $$p=P_{\infty}\tag{6}$$Solving Eqns. 5 and 6 for the radial displacement at the cavity gives: $$u_a=\frac{(P_a-P_{\infty})}{4G}a\tag{7}$$ From this, it follows that $$\sigma_r=-P_{\infty}-(P_a-P_{\infty})\frac{a^3}{r^3}$$ $$\sigma_{\theta}=\sigma_{\phi}=-P_{\infty}+\frac{(P_a-P_{\infty})}{2G}\frac{a^3}{r^3}$$$$\epsilon_r=-\frac{(P_a-P_{\infty})}{2G}\frac{a^3}{r^3}$$$$\epsilon_{\theta}=\epsilon_{\phi}=\frac{(P_a-P_{\infty})}{4G}\frac{a^3}{r^3}$$ The strain energy density $W$ can be written $$W=\frac{\sigma_1\epsilon_1+\sigma_2\epsilon_2+\sigma_3\epsilon_3}{2}=\frac{\sigma_r\epsilon_r+2\sigma_{\theta}\epsilon_{\theta}}{2}.$$ Therefore $$W=3\frac{(P_a-P_{\infty})^2}{8G}\left(\frac{a}{r}\right)^6.$$ The strain energy stored in the pressure vessel, $U$, can then be found by integrating over the volume, $$U=\int_V W dV = 4\pi \int^{\infty}_{r=a} W(r) r^2 dr = 3\frac{\pi (P_a-P_{\infty})^2 a^6}{2G}\int^{\infty}_{r=a}\frac{1}{r^4}dr,$$ so finally $$U=\frac{\pi (P_a-P_{\infty})^2}{2G}a^3.$$