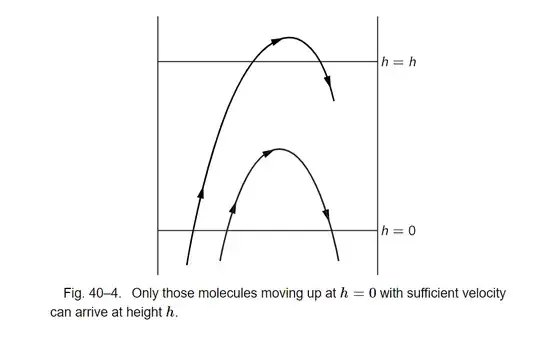
In Feynman's treatment of statistical mechanics, $40–4$ The distribution of molecular speeds, Feynman analyzes a gas at thermal equilibrium, and derives the distribution of the velocity of its molecules, he writes,
Let us count how many molecules are passing from below to above the plane $h=0$ (by calling it height$=0$, we do not mean that there is a floor there; it is just a convenient label, and there is gas at negative h). These gas molecules are moving around in every direction, but some of them are moving through the plane, and at any moment a certain number per second of them are passing through the plane from below to above with different velocities. Now we note the following: if we call $u$ the velocity which is just needed to get up to the height $h$ (kinetic energy $mu^{2}/2=mgh$), then the number of molecules per second which are passing upward through the lower plane in a vertical direction with velocity component greater than $u$ is exactly the same as the number which pass through the upper plane with any upward velocity. Those molecules whose vertical velocity does not exceed $u$ cannot get through the upper plane. So therefore we see that $$\begin{equation*} \text{Number passing }h = 0 \text{ with }v_z > u = \text{number passing }h = h \text{ with }v_z > 0. \end{equation*}$$
But the number which pass through $h$ with any velocity greater than $0$ is less than the number which pass through the lower height with any velocity greater than $0$, because the number of atoms is greater; that is all we need. We know already that the distribution of velocities is the same, after the argument we made earlier about the temperature being constant all the way through the atmosphere. So, since the velocity distributions are the same, and it is just that there are more atoms lower down, clearly the number $n_{>0}(h)$, passing with positive velocity at height $h$, and the number $n_{>0}(0)$, passing with positive velocity at height $0$, are in the same ratio as the densities at the two heights, which is $e^{−mgh/kT}$. But $n_{>0}(h)=n_{>u}(0)$, and therefore we find that
$$\begin{equation*} \frac{n_{> u}(0)}{n_{> 0}(0)} = e^{-mgh/kT} = e^{-mu^2/2kT}, \end{equation*}$$
$\\$
As he mentioned it, the density of the gas, which he derived two sections before, is $n(h)=n_{0}e^{-mgh/kT}$, where $h$ is the height and $n_{0}$ is the density at $h=0$.
Even under the assumption that the velocity distribution is homogeneous, which he didn't really give a proof for, why is it that the ratio $n_{> 0}(h) /n_{> 0}(0)$ must be the same as the density ratio, which is equal to $e^{-mgh/kT}$?