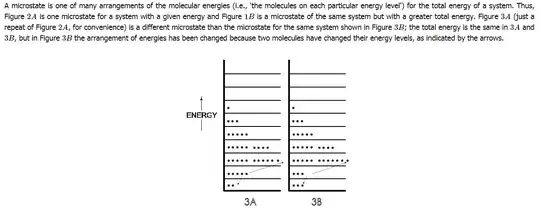
Why various molecules in an ideal gas at a particular temperature can have only quantized energies?

Question

1. Why various molecules in an ideal gas at a particular temperature can have only quantized energies? Why can't they have the energies distributed in a continuous fashion?

Following is an image taken from the mentioned reference, where it shows that various molecules can take only certain energies and not the energies in between those levels. What is the reason behind such quantization of energy in gas molecules?

The same idea Prof. Peter Atkins also talks about in his book "Very short introduction to Thermodynamics", but in the book, he did not explain the reason behind it.

2. How do we know that such energy levels are there?

3. What do we lose if we assume the distribution of energy to be continuous?

Reference: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Thermodynamics/Energies_and_Potentials/Entropy/The_Molecular_Basis_for_Understanding_Simple_Entropy_Change

Answer 1

To answere your first question:

Due to the assumption that the ideal gas is in a closed body (mostly a cube with edge length L for easier calculation) the wave function of e.g electrons, considering a fermi-gas, need to fullfill certain boundary conditions. For the energy you then get that it needs to be quantized since there are different modes/quantum numbers for the solution of the Schroedinger equation.

You can look at the wavefunction of the particles analogous to a guitar string with fixed ends.

Answer 2

The picture and the explanation do not require that the energy levels are discreet. The picture is often shown / described this way for simplicity. The separation can just as well be infinitesimal (zero).

• The three modes of storing internal energy in a gas are translation, rotation, and vibration. An ideal gas particle has zero volume and therefore has only translation. In an unconfined system, the separation between translation levels is infinitesimal (zero). In a finite-sized system where the collisions between particles dominates the collisions to the walls, the gas particles still behave classically. At the point where the gas particles collide with the walls more often than each other, the levels can become discreet (quantized). This is analogous to the particle-in-a-box state of quantum mechanics. See this link for further insight about molecular speed distributions.

• Rotation and vibration levels appear in molecules. Their energies are quantized. The energy distribution that you show applies.

• We loose nothing to translate from discreet to continuous. We translate the math from summations to integrals. We obtain a continuous distribution function rather than a discreet set of levels. Here for example is the continuous distribution plot of speed and kinetic energy for molecular oxygen at 150 °C.