Suppose we have an object swinging by a black hole. My understanding is that if it remains outside the black hole, it just swings by and doesn't lose any energy (except maybe gravitational waves?). But if it enters the event horizon, it's gone forever. i.e. the blue trajectory in the picture is possible, but the red one isn't.
How does this work? How does the object on the red trajectory lose its kinetic energy? Is it an "all or nothing" thing where the object will retain all its energy unless it dips into the event horizon and then lose it all? Or does the object gradually lose more energy as it gets closer to the event horizon?
Edit:
Thank you to the respondents. Summary (if I've understood correctly - please correct me if not) is:
In Newtonian physics, a small object orbiting a big object without losing energy will follow either an ellipse or hyperbola, depending on the speed. What goes down, must come up. In Relativity, this is not True - objects follow Schwarzchild geodesics - and the difference from Newtonian orbits becomes larger as we get very close to very massive objects. Neither the "red" nor the "blue" object in the below image loses its energy - in relativity, objects can spiral in without losing energy.
Re: The all-or-nothing thing. There exists a sphere (the Photon Sphere - dotted line on below image) outside the event-horizon, where any photon entering it will eventually spiral into the black hole. So at least for massless objects, if the object dips into the photon sphere, it's in for good.
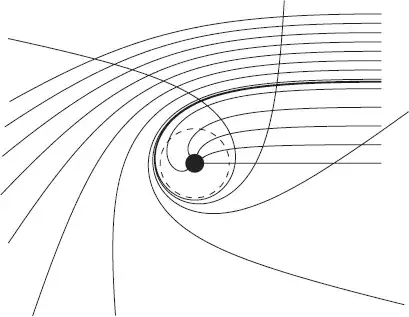
Image of Schwartzchild geodesics near a black hole from General-Relativistic Visualization.What happens to the red object after falling past the event horizon depends on who's watching. For an outside observer, the red object will just park at the event horizon and hang out there forever. For the observer aboard the red object, it will just cross the event horizon and hit the singularity in a finite (and small) time. After that, the rules don't say what happens.

There appears to be some controversy on that last point (at least in the answers below). Some seem to argue that an observer on the red object ceases to exist once it hits the event horizon, rather than the singularity (i.e. the left image above is also true for the observer on the red trajectory). It may be a moot point since there's no way to verify this.
