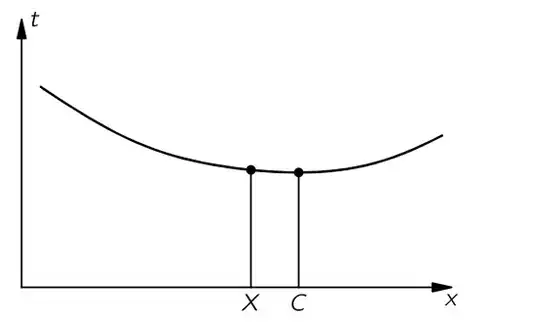
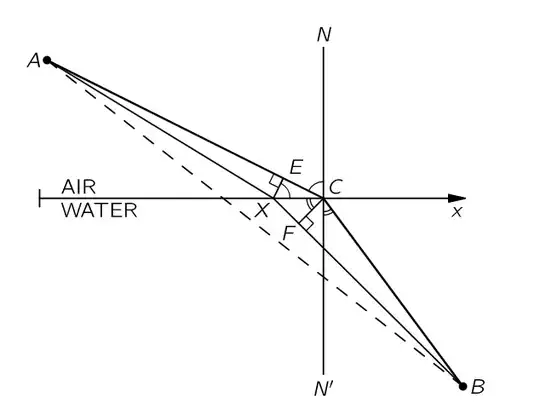
In this lecture about Fermat's principle, Feynman derives the refraction law using the principle of least action. He finds the shortest path between $A$ and $B$ by defining a variable point $X$ and setting its distance to the point corresponding to the shortest path, $C$, to zero. He said,
If we were to plot the time it takes against the position of point X, we would get a curve something like that shown below, where point C corresponds to the shortest of all possible times. This means that if we move the point X to points near C, in the first approximation there is essentially no change in time.
In deriving Snell's law, he used the following approximation:
$$ \angle XCF\approx \angle BCN' ~~~(\text{when $X$ is near $C$}),$$
Where did this approximation exactly come from?