In mathematical physics and other textbooks we find the Legendre polynomials are solutions of Legendre's differential equations. But I didn't understand where we encounter Legendre's differential equations (physical example). What is the basic physical concept behind the Legendre polynomials? How important are they in physics? Please explain simply and give a physical example.
4 Answers
The Legendre polynomials occur whenever you solve a differential equation containing the Laplace operator in spherical coordinates with a separation ansatz (there is extensive literature on all of those keywords on the internet).
Since the Laplace operator appears in many important equations (wave equation, Schrödinger equation, electrostatics, heat conductance), the Legendre polynomials are used all over physics.
There is no (inarguable) physical concept behind the Legendre polynomials, they are just mathematical objects which form a complete basis between -1 and 1 (as do the Chebyshev polynomials).
- 1,805
Here's my 30 seconds hand waving argument for
"Why is it that we always encounter new special functions $f_n$ with orthogonality relations??"
$$\int f^*_n\cdot f_m=\delta_{mn}$$
Super broadly speaking, in physics we dealing with the dynamics of certain degrees of freedom. These often employ smooth symmetries, that is we're dealing with Lie groups, which are also manifold in themselfs. Take e.g. the Laplacian $\Delta=\nabla\cdot\nabla$ and the associated symmetries $R$ acting as $\nabla\to R\nabla$ in such a way that that $R\nabla\cdot R\nabla=\nabla\cdot\nabla$.
Now in case one is dealing with a "rotation" in the broadest sense of the word, one often has a compact manifold, where we can savagely define things like integration on the group, and these symmetry groups also permit pretty unitary matrix representations. That is there are necessarily matrices $U$ with
$$\sum_kU_{kn}^*U_{km}=\delta_{mn},$$
and well, the matrix coefficients $U_{kn}$ must be some complex functions.
To put it short, special functions are representation theory magic.
@zonk: Yes, it's the default theory. But of course, you only see the direct relation to special functions if you take the abstract Lie group theory and actually sit down and write down the matrices in some base. E.g. for the rotation group matrices $D$, you find
$$ \begin{array}{lcl} D^j_{m'm}(\alpha,\beta,\gamma)&=& e^{-im'\alpha } [(j+m')!(j-m')!(j+m)!(j-m)!]^{1/2} \sum\limits_s \left[\frac{(-1)^{m'-m+s}}{(j+m-s)!s!(m'-m+s)!(j-m'-s)!} \right.\\ &&\left. \cdot \left(\cos\frac{\beta}{2}\right)^{2j+m-m'-2s}\left(\sin\frac{\beta}{2}\right)^{m'-m+2s} \right] e^{-i m\gamma} \end{array}.$$
Very sweet, right? Now here you have the Legendre Polynomials $P_\ell^m$
$$ D^{\ell}_{m 0}(\alpha,\beta,0) = \sqrt{\frac{4\pi}{2\ell+1}} Y_{\ell}^{m*} (\beta, \alpha ) = \sqrt{\frac{(\ell-m)!}{(\ell+m)!}} \, P_\ell^m ( \cos{\beta} ) \, e^{-i m \alpha } $$
so that
$$ \int_0^{2\pi} d\alpha \int_0^\pi \sin \beta d\beta \int_0^{2\pi} d\gamma \,\, D^{j'}_{m'k'}(\alpha,\beta,\gamma)^\ast D^j_{mk}(\alpha,\beta,\gamma) = \frac{8\pi^2}{2j+1} \delta_{m'm}\delta_{k'k}\delta_{j'j}.$$
- 8,873
Rather than thinking about the abstract orthonormal basis of the Legendre polynomials $P_l(x)$, I find it easier to visualize these polynomials by looking at $P_l(\cos\theta)$. These are simply the Spherical Harmonics with azimuthal symmetry:
$$ Y_l^{m=0} = n_l P_l(\cos\theta)$$
where $n_l$ is a normalization factor that only depends on $l$. In this beautiful image of the spherical harmonics on Wikipedia by Inigo.quilez, the $P_l(\cos\theta)$ correspond to the center column of the image ($m=0$). Note the symmetry about the $z$-axis.
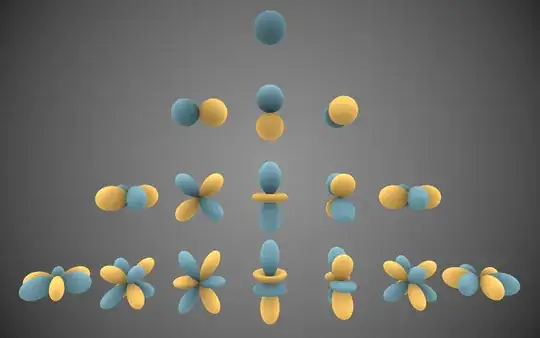
These are come up very often in physics, for example, while solving the Laplace equation ($\nabla^2\Phi = 0$) with azimuthally symmetric boundary conditions.
- 489
If you want to know why computational physicians like Legendre Polynomials, the answer is rather simple. As the other people has already pointed out, the Legendre Polynomials are orthogonal, they can be a very good basis for many applications. For example, if one tries to construct a function which fits the experiment or simulation data within the estimate error-bar and interpolates between the limited number of available data points, the Legendre Polynomials can be a very useful, so does the Chebyshev polynomials. The function constructed from the the Legendre Polynomials does not suffer the Runge's problem.
- 43