Derivation of reduced mass

Question

Why is it true, that if you have a system of two stars for example, moving around the centre of inertia of the system due to gravitation, these stars can be replaced by a single star of mass $$\mu=\frac{m_1m_2}{m_1 + m_2}$$ where $m_1$ and $m_2$ are the masses of the initial stars?

Answer 1

Two body system can be analyzed more simply using reduced mass, as problem basically reduces to single body. The first approximation can be obtained by assuming that, m1>>m2, such as planet orbiting the star, because center of gravity coincides with m1. Thus it can be assumed that the heavy body is at rest and lighter one moves around it.

Derivation: $$\text{Let}\,m_1,\vec r_1\text{be a mass and position of the massive body and}\,m_2,\vec r_2\,\text{the lighter one.}$$

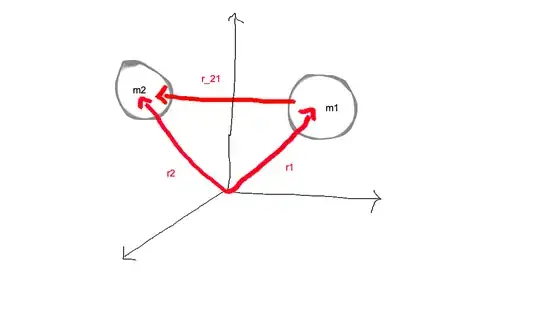$$\text{It is assumed that}\, m_1>>m_2\,\text{The force between the masses (gravity) depends on difference of positions vectors}:\vec F_{12}=\vec F(\vec r_{12}), \text{where}:$$

$$\vec r_{21}=\vec r_2-\vec r_1\\ \vec F_{12}\,\text{is force on body 1 due to body 2}$$ In our approximation we assume the heavy mass is at rest at origin. Thus: $$\vec r_{21}=\vec r_2$$ And equation of motion becomes: $$\vec F(\vec r_{21})=m_2\frac{d^2\vec r_{21}}{dt^2}=m_2\frac{d^2\vec r_{2}}{dt^2}$$ which can be solved to obtain position.

To obtain 'true' motion, it turns out our approximation can be made exact by considering center of mass(CM).(which is a mass weighted average of the positions of two masses in this case) $$\vec R_{CM}=\frac{m_1\vec r_1+m_2\vec r_2}{m_1+m_2}=\frac{m_1\vec r_1}{m_1+m_2}+\frac{m_2\vec r_2}{m_1+m_2}$$ $$\text{We will call quantity}\frac{m_2m_1}{m_1+m_2}=\mu\,\text{reduced mass}$$ $$\text{Thus}: \vec R_{CM}=\frac{\mu\vec r_1}{m_2}+\frac{\mu\vec r_2}{m_1}$$ It can be easily shown that net external force on the system equals the total mass times the acceleration of the center of mass. If you are not convinced, I have written before such derivation in this POST

Since it is assumed no external forces are present (the force of gravity between masses 'counts' as internal one), center of mass moves at constant velocity. $$\frac{d^2\vec r}{dt^2}=0\implies\frac{d\vec r}{dt}=const.$$ Let CM be taken as origin of an inertial coordinate system. Thus position of the two masses is given by: $$\vec R_{CM}=0\implies\frac{\mu\vec r_1}{m_2}=-\frac{\mu\vec r_2}{m_1}\implies \vec r_1=-\frac{m_2\vec r_2}{m_1};\,\vec r_2=-\frac{m_1\vec r_1}{m_2}$$ $$\text{Since}:\vec r_{21}=\vec r_2-\vec r_1\,\text{we get:}$$ $$\vec r_{21}=-\frac{m_1}{m_2}\vec r_1-\vec r_1=-\vec r_1(\frac{m_1+m_2}{m_2})\implies \vec r_1=-\frac{\mu}{m_1}\vec r_{21}$$ $$\vec r_{21}=\vec r_2+\frac{m_2}{m_1}\vec r_2=\vec r_2(\frac{m_1+m_2}{m_1})\implies \vec r_2=\frac{\mu}{m_2}\vec r_{21}$$ $$\text{Therefore equations of motion are}:$$ $$\vec F(\vec r_{21})=m_2\frac{d^2\vec r_{2}}{dt^2}=\mu\frac{d^2\vec r_{21}}{dt^2}$$ $$\vec F(\vec r_{12})=\vec F(-\vec r_{21})=m_1\frac{d^2\vec r_{1}}{dt^2}=-\mu\frac{d^2\vec r_{21}}{dt^2}$$ Which is our equation obtained previously in our approximation with reduced mass. Note that if m1>>m2 reduced mass is almost the same as m2.

This the motion of two body system consists of its CM and motion around it. The motion around it can be described in terms of a single, reduced mass moving around fixed center.