Gravitational force decreases with depth under the surface of Earth, and at centre, the surrounding forces cancel each other out effectively making it zero and hence a body at the center of gravity of the Earth (which would be very close to the centre of the Earth, the core) would experience weightlessness. Now the famous study in 2016 (https://arxiv.org/abs/1604.05507) says that the core is 2.5 years younger than the crust even though the former was formed first, due to gravitational time dilation causing the core to age slower even though the gravity acting on the core should be lower than what is on the crust. I understand that I might be confusing myself between two scientific principles but I want to understand both and know where my understanding is wrong.
4 Answers
The confusion comes from a common misinterpretation that "time dilation is caused by gravity". In fact, the relation is the opposite. Time dilation, as as part of spacetime curvature, causes gravitational attraction. In a nutshell, while moving forward in time, things shift to where time runs slower, so (in a simplified view) gravity is defined by the gradient of the time dilation. This gradient is zero at the center of the Earth, so the gravitational attraction there is zero despite the time dilation being maximal.
Another common misconception is a misinterpretation of the Brinkhoff theorem, a relativistic version of the Newton shell theorem. The Newton theorem says that gravity caused by an empty massive spherical shell is zero inside, so gravity there is defined only by masses present inside. However, in General Relativity, spacetime inside such a shell s defined by both the masses inside and by the shell. For example, if the time dilation at the (inner) surface of the shell is such that time there runs twice slower than at infinity, then the time dilation inside the shell is the same everywhere and, due to the zero gradient, there is no gravitational force anywhere inside despite all things there agng twice slower.
- 13,017
Assuming the current understanding of Earths composition and formation , according to GR this is true up to the exact number of days/ years. I remember Feynman making a similar remark as an example of application of relativity. Let's say you are born in the center of a massive body and moved to the surface. Eventually as time is running more slowly for you, you would overtake your parents in age given enough time and relativity to work.
- 111
Possible answer: Gravity inside a spherical body with radius $a$ and constant density $\rho$ obeys the metric
$$d{{s}^{2}}=\left( 1-(1/3)\rho a^2 \right)d{{t}^{2}}-\frac{d{{r}^{2}}}{1-(1/3)\rho r^2}-{{r}^{2}}(d{{\theta }^{2}}+{{\sin }^{2}}\theta \,d{{\phi }^{2}}),$$
when choosing units of measurement convert the light velocity $c$ and the gravitational constant $G$ into $c=8\pi G =1$ Cambridge Open Engage.
This approach is based on the assumption that distributed matter excites a negative vacuum pressure $p = -(1/3)\rho $ (see also Rom. Rep. Phys. 72, 113 (2020)).
In standard units, this metric has the form
$$d{{s}^{2}}=\left( 1-\frac{8\pi G}{3c^2}\rho a^2 \right)d{{t}^{2}}-\frac{d{{r}^{2}}}{1-\frac{8\pi G}{3c^2}\rho r^2}-{{r}^{2}}(d{{\theta }^{2}}+{{\sin }^{2}}\theta \,d{{\phi }^{2}}).$$
The flow of time inside the sphere is constant and coincides with one on the surface. Time flows more slowly than at a distance from the sphere in $\left( 1-\frac{8\pi G}{3c^2}\rho a^2 \right)^{1/2}$ times.
The Earth consists of several regions, the density in which differs significantly.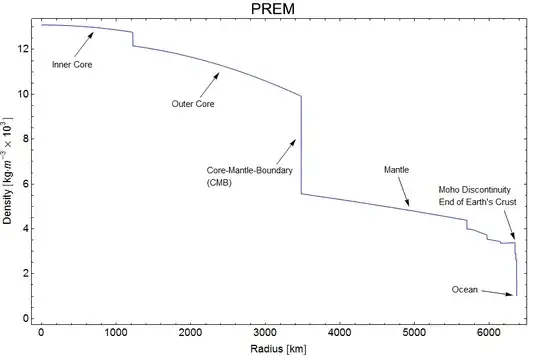 
We consider the core density to be approximately $\rho_{co}=11000 kg/m^3$ and the density of the outer region, which includes the mantle and crust, $\rho_{out}=4400 kg/m^3$. In this case, the gravitational field inside the Earth will be the sum of the fields of two spheres with $\rho_1=\rho_{out}, a_1=a_E=6378 km$ and $\rho_2=\rho_{co}-\rho_{out}=6600 kg/m^3, a_2=a_{co}=3488 km$. The effect of time dilation in the center of the Earth will be the total of 2 spheres. The relative difference between the time in the absence of gravity and in the center of the Earth will be $8.05*10^{-10}$. The course of time in the center will differ little from the course of time in the entire region of the core. In the region of the mantle, it will begin to approach the surface. The relative difference between the clock readings in the center of the Earth and on the surface is $1.09*10^{-10}$.
- 11
- 4
According to a paper at the following link: https://ui.adsabs.harvard.edu/abs/2007AGUFM.V33A1161P/abstract the earth's crust is 2.77X10^22 kg. The mass of the core, from information obtained on the structure of the earth article on Wikipedia (https://en.wikipedia.org/wiki/Structure_of_the_Earth#Core) is 2.15X10^24 kg, approximately. (I'll let you calculate this number and check my work. You'll want the radii of the inner and outer core, the formula for volume of a sphere, and the lower limits on density of the inner and outer core, then sum the total masses of the inner and outer core together). Even if my math is off by just a little bit, the point is that the earth's core is more massive than the crust by at least 2 orders of magnitude. This means that the gravitational force near the core will be quite a bit stronger than at the surface of the crust, so yes, the crust would be older than the core, as time dilation from the higher gravitational field, means that less time will have passed for the core, than for the crust.
I hope this helps, and also, if I didn't format the math correctly, could someone be so kind as to fix my post so that the math is coded correctly? Thanks.
