All other fundamental forces are mediated by vector bosons. The Higgs boson is a scalar boson & the interaction it mediates isn't called as a force. A force is a vector in the usual description. But the hypothesized graviton is a tensor boson. Would that mean gravity is not a usual force but may be a generalization of the concept of force into a tensor? (Einstein field equation relates Einstein tensor & stress-energy tensor & therefore sort of relates curvature & energy. And gravity is curvature).
3 Answers
Force is a concept coming from the classical level, is always a vector, and is given by the vector dp/dt. The spin of the particular gauge boson does not touch the concept of force even at the quantum level.
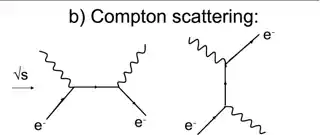
In any interaction the exchange has a dp/dt, and it is a force whether a Higgs particle comes out, or any other particle or complex of particles from the particle table. A clear example is compton scattering, where the exchanged particle that generates the fourvector exchange is an off mass cell electron, neither a vector nor a tensor. A dp/dt though is well defined for a "force"
The reason the gauge bosons are identified with the corresponding force is because the lowest order diagrams for that interaction involve the gauge bosons, introducing the coupling constants which differentiate the interactions. But the force per se is always a vector.
- 236,935
Gravity is a vector force in disguise.
The metric $g_{\mu\nu}$ is the "multiplication" of two tetrad vectors $e_\mu$ and $e_\nu$. The vectorness is embedded surreptitiously inside metric.
What Dirac serendipitously stumbled upon in 1928 were the "square roots" of the flat metric $\eta_{\mu\nu}$, where vierbein/tetrad vectors $e_\mu$ are simply Gamma matrix "vectors" $e_\mu = \gamma_\mu$: $$ \eta_{\mu\nu} = \frac{1}{4}\mbox{Tr}(\gamma_\mu\gamma_\nu), $$ where $\mbox{Tr}(M)$ denotes the trace of a square matrix $M$.
The "square roots" of curved space time metric $g_{\mu\nu}$ are vierbein/tetrad vectors $e_\mu$, which are linear combinations of the Gamma vectors: $$ e_\mu = e^a_\mu(x)\gamma_a, $$ where the linear combination coefficients $e^a_\mu(x)$ are space time dependent numbers (not matrices!) .
The curved space time metric $g_{\mu\nu}$ is thus expressed as the "multiplication" of two tetrad vectors $e_\mu$ and $e_\nu$: $$ g_{\mu\nu} = \frac{1}{4} \mbox{Tr}(e_\mu e_\nu) = \frac{1}{4} \mbox{Tr}(e^a_\mu\gamma_a e^b_\nu\gamma_b) = e^a_\mu e^b_\nu (\frac{1}{4} \mbox{Tr}(\gamma_a \gamma_b)) = e^a_\mu e^b_\nu \eta_{ab}. $$
Added note:
If one prefers pure geometric algebra terminology over matrix representation. One can replace the trace of matrices with $$ \frac{1}{4}\mbox{Tr}(\ldots) \rightarrow \langle\ldots\rangle, $$ where $\langle\ldots\rangle$ denotes the scalar portion of the enclosed multivector, which reduces to dot product in case of multiplication of two vectors: $$ \langle e_\mu e_\nu\rangle = \frac{1}{2}(e_\mu e_\nu + e_\nu e_\mu) = e_\mu . e_\nu $$
Henceforth $$ g_{\mu\nu} = \langle e_\mu e_\nu\rangle= e_\mu . e_\nu . $$
More added note to address comments regarding Weinberg-Witten theorem:
The Weinberg-Witten theorem is usually interpreted to mean that the graviton cannot be a composite particle in a relativistic quantum field theory. However, the theorem's implication of non-compositeness is predicated on "no fundamental diffeomorphism symmetry". The vierbein/tetrad formulism as described in this answer DOES enjoy the fundamental diffeomorphism symmetry, therefore the purported proof of non-compositeness does NOT apply.
- 5,451
- 13
- 42
I think you are too attached to the usual "vector boson" theories. From the Effective Field Theory point of view, Einstein's gravity is just the theory of a massless spin 2 particle (the graviton), which $\textbf{must}$ be embedded into a symmetric rank-2 tensor. In such theory, all particles that carry energy interact with the graviton. The potential in this QFT framework is defined as usual, as the amplitude of two particles exchanging gravitons.
In other words, I mean that in the moment one steps in QFT and begins to understand particles as excited states of fields that bear well defined representations of the Lorentz group, one must also put aside classical concepts like force. In both QM and QFT what matters is the potential energy between two (or more) particles, which will in turn dictate their dynamics. Such potentials can be calculated using the appropriate interactions between the particles; if they are mediated by scalars, vector, tensor or even fermions does not matter at all.
- 159
- 6