They may in special cases, but this is by no means a rule, and most certainly doesn't hold for all cases. As I'm a firm believer in concrete examples, I'll illustrate this with the following simple case of two blocks, each of mass $m_1=m_2=m$, connected to walls and each other by Hookean springs (which are harmonic oscillators) of spring constant $k$, as shown in the following image
$$$$
Now, the Lagrangian for this system is, of course, $$L=\frac{1}{2}m\left(\dot{x}_1^2+\dot{x}_2^2\right)-\frac{1}{2}kx_1^2-\frac{1}{2}k\left(x_2-x_1\right)^2-\frac{1}{2}kx_2^2$$
which returns the equations of motion $$\begin{align}
\ddot{x}_1 &=-\frac{2k}{m}x_1+\frac{k}{m}x_2 \\
\ddot{x}_2 &=\frac{k}{m}x_1-\frac{2k}{m}x_2\\
\end{align}$$
One can solve these equations with a bit of linear algebra, and one gets, with vanishing initial velocity,
$$\begin{align}
x_1(t) &= \frac{1}{2}\left(x_1(0)+x_2(0)\right)\cos\left(\sqrt{\frac{k}{m}}\,t\right) +\frac{1}{2}\left(x_1(0)-x_2(0)\right)\cos\left(\sqrt{\frac{3k}{m}}\,t\right) \\
x_2(t) &=\frac{1}{2}\left(x_1(0)+x_2(0)\right)\cos\left(\sqrt{\frac{k}{m}}\,t\right) -\frac{1}{2}\left(x_1(0)-x_2(0)\right)\cos\left(\sqrt{\frac{3k}{m}}\,t\right)
\end{align}$$
Now, even this simple case isn't periodic except in cases where $x_1(0)=x_2(0)$ or $x_1(0)=-x_2(0)$, as the terms in the cosines differ by a factor of $\sqrt{3}$. This nonperiodicity as can be seen in these plots, where I have set $k=1.2321$, $m=0.771203$, $x_1(0)=e+0.231$, and $x_2(0)=1$.
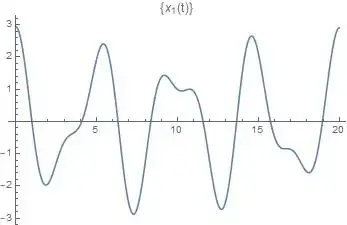
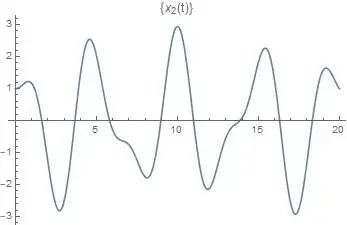
There are many, many more examples I could show. In general, the motion of coupled oscillators is complex, is not necessarily periodic, and does not tend toward rational frequencies. Now, are there cases where the motion is periodic and they are in sync? Of course, but they are not the general rule. For this example, set $x_2(0)=-x_1(0)$, and they are in a ratio of $1:1$, as shown in the below plots (everything is the same, except $x_1(0)=-1$).
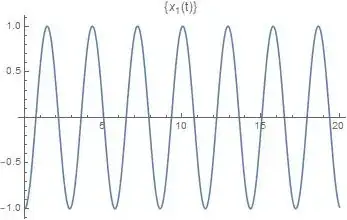
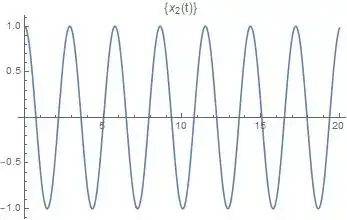
To sum it up, while there are some cases where oscillators tend towards being in a rational sync, this is not always true.
