I hope this is the right place to ask this question.
Suppose I found a small irregular shaped rock, and I wish to find the surface area of the rock experimentally. Unlike for volume, where I can simply use Archimedes principle, I cannot think of a way to find the surface area. I would prefer an accuracy to at least one hundredth of the stone size.
How can I find the surface area experimentally?
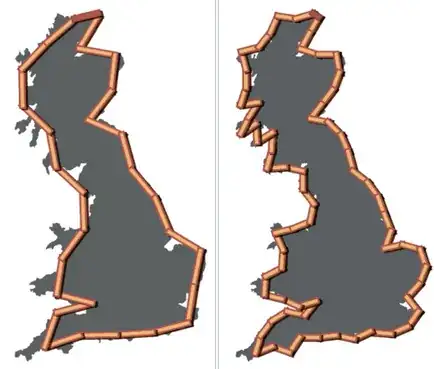
I would ignore answers that say the surface area is ill-defined. In any realistic situation you have a lower limit for how fine a resolution is meaningful. This is like a pedant who says that hydrogen has an ill-defined volume because the electron wavefunction has no hard cutoff. Technically true, but practically not meaningful.
My recommendation is an optical profilometer, which can measure the surface area quite well (for length scales above 400nm). This method uses a coherent laser beam and interferometry to map the topography of the material's surface. Once you have the topography you can integrate it to get the surface area.
Advantages of this method include: non-contact, non-destructive, variable surface area resolution to suit your needs, very fast (seconds to minutes), doesn't require any consumables besides electricity.
Disadvantages include: you have to flip over your rock to get all sides and stitch them together to get the total topography, the instruments are too expensive for casual hobbyists (many thousands of dollars), no atomic resolution (but Scanning tunneling microscopy is better for that).
The optics for these instruments look like below
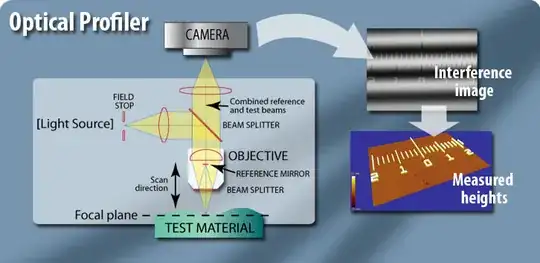
And it gives a topographic map like below.
(source: psu.edu)
The problem is that as you increase the measurement precision, so will increase the result you get. The result of a meaningful experiment should converge with the increase of the precision, this does not.
This is a 3D analogy of the coastline paradox: the surface of the rock is fractal-like, just like the coasts of the countries:
The result will say more from your measurement precision, than from a real surface area.
Obviously if the stone is not very fractal-like (like it is a sphere, or a skulpture), then the result will converge, but not this is the general case in practical stones.
The way I would do it is to first dip the rock in thinned fingernail polish. Let that dry, and then dip the rock into hot liquid wax. Let the wax cool. Peel the wax off the rock and measure the thickness of the wax layer. Melt the peeled-off wax and measure its volume. Divide the volume by the thickness, and you have the area.
I would prefer an accuracy to at least one hundredth of the stone size.
Divide the weight of the stone's paint by the weight of the square's paint to get the surface area of the stone.
This assumes you've defined the "surface area" of a real object, and "the stone size" means a circle of diameter equal to the largest diameter of the stone (or some other reasonable interpretation).
Instead of soot, you could also use spray paint, but it would likely sip into the crinkles more. Or you could wrap in paper instead of alu and use a pencil, but that would smear and be harder to see on the photo.
I don't think this method will get 1/100 accuracy, but it gives at least a decent estimate and doesn't require special equipment.
The task isn't well-defined. Do you include cracks? If yes, you'll see finer and finer cracks adding to the surface, and in the end you'll be at atomic level and find it hard to even define what's part of the rock and what isn't. If you don't include cracks: What's your rule for distinguishing a mere unevenness from a crack?
Difficult. Adsorb some chemical, heat it up, measure the amount that evaporates?
I would look at the literature, maybe start with a search for "experimental determination of the surface area" in geological contexts.
Edit: a molecular probe should give something close to the maximum value. There is an end to the length scale when dealing with real materials, a rock is not a mathematical fractal. After letting in a suitable kind of molecules and pumping them out, thermally stimulated desorption would measure the absorbing area.
For non-convex bodies of arbitrary shape, as many people already pointed out, there is no reasonable answer in general. For convex bodies the answer is mathematically and physically well defined. The method is based on integral geometry, if I remember right, the formula is due to Steiner or Crofton. Nevertheless it is a practical method, and stable. The formula gives the surface area in terms of the (average area) of the projection of the body along all directions $\vec{n}$: $$ S = \frac{1}{\pi} \int d\Omega_{\vec n} ~ S(\vec n) = 4 \times \left< S(\vec n) \right>$$ So all you need to do is place a lamp high above, hold the stone in many random directions, calculate the average area of the shadow, and multiply by 4. For 1% accuracy, ten thousand (10,000) random projections will be enough.
I'm vouching for vapor deposition or application of coating which can be measured by weight.
Depends on your rock size. Open cell pumice and porous limestone bored by rain and animals will be difficult to measure. Limestone can be micro-porous and can have hundreds of square meters of surface area. Consider this micrograph of chalk.
Using a substance that adheres strongly and evenly to the surface of rocks regardless of their pH and chemical affinities, vapor-treat or dip the rock in the coating substance, use an effective way of removing the excess, and weigh the rock/substance afterwards. Perhaps you can get a degree of precision if there is a substance which can be applied in a perfectly even coat for all the different samples.
For the first attempt, I'd use water-vapour. Weigh the rock dry, subject it to a few moments in a high-humidity environment, and weigh it again afterwards.
Take a lot of pictures from different angles that enable you to create a 3D mesh using photogrammetry (I recommend Meshroom). You could also use a LIDAR to capture the point-cloud then use Meshroom to mesh it (apparently there are some cheap ones from less than 2000 dollars). Calculate the area of the mesh (I recommend Rhinoceros3d). There are many open-source tools that can help you with the process. EDIT: someone already gave a similar answer, so I added some software recommendations (I know they are usually out of place for stackexchange but if OP really wants to sove the problem rather than hypothetically post a cool question the recommendations could be handy). If you are going the photogrammetry way, remember that if the surface is specular you will need to coat it in a diffuse paint.
Similar to the gas adsorption/BET and @McGrew wax technique. You would need a sensitive scale with centigram precision.
You can also measure the location of points on the stone for some fixed point say the (0,0,0) point in close proximation.
Map the points using Octave (free and open-source) or Matlab Mathematical software. Form 3d triangle meshes with that point. Compute the area of the triangles. Add them. And that's it. The Surface Area.
If you have access to a planimeter, then you might try the method used in this research paper on the strength of cements used on teeth.
In order to compare the strength of the cement, the authors needed to separate the effect due to the cement from effect due to the varying surface areas of the real teeth used in the tests.
For each tooth used, the authors laid aluminum foil over the teeth and used a burnishing tool to make the foil follow the contour of the surface of each tooth. Overlapping areas were then cut away and the foil was removed from the the tooth then pressed flat. A tracing of the outline of each piece of foil was made, and the area measured using a planimeter.
I happen to have bought a planimeter of the exact same model as used in the referenced paper, and actually found that paper while searching the internet for information about the planimeter I had just bought at a fleamarket.
You can put the rock in an MRI scanner and get a 3D profile of it (and therefore, the volume and surface area). If it doesn't have spins that are useful for NMR, you can dunk the rock in something that does (ie. water or mineral oil), and then image that, and the void will give you the 3D profile of the rock (which you can then use to calculate the area).
The main problem of using NMR is that if the magnetic susceptibility of your rock is very different than that of vacuum... you will get image artifacts. But there are tricks around this though.
As an example: here is a lithium dendrite inside a battery imaged using MRI.
Alternatively, you can use Xray images of your rock from many different angles and reconstruct the 3D profile of the rock using the inverse 3D Radon Transform. Having the 3D profile, you can easily calculate the area.
because the rock is in irregular shapes (mostly), it is hard to use some normal surface measuring method for the regular 3-D objects. Of course one can use closed integrals to go calculation, but that is boring. it will be easier if we can change the 3-D object surface into 2-D.
I will recommend if you have a bucket of sticky fluid, you can dip the rock into it and let it dry. then use some papers to fit into it and you can get the result. however, this is not accurate.
I will more recommend you to scan the rocket into 3-D models to make the computer do the job using accurate algorisms.
In most cases like this, the best option is to scan the object into a dense cloud somehow and measure the approximate surface area using the tools provided. Although I am certain that a variety of exotic methods exist for generating dense clouds, your best options would be to either use a LIDAR unit of some kind or to use a camera and a photogrammetry program. Depending on how detailed you want your estimate to be, you could use anything from a dedicated 3D scanning setup to a few tens of photos taken on your phone and one of many free photogrammetry programs.
I would use rice or sand, With the volume measured you can measure the area by pouring the sand or rice into a flat tray and making sure that you have a one-grain thickness carried over the tray, You will then be able to not only see the physical representation but measure it as well. I have done this many times myself when figuring out the outer surface areas of my parts.
Here's a more solution-oriented answer which takes the clarification into account:
This is essentially equivalent to the wax method, except electroplating is not affected by gravity.
I am a bit hazy about how to best measure the amount of metal; please feel free to suggest improvements or directly edit this answer.
The most direct approach I can think of would be to measure the loss of metal on the counterelectrode.
Do you want to restore the stone to its pre-measurement state?
You'd probably select a metal and a paint that are easy to remove.
Again, somebody with more practical knowledge of electroplating may be able to help with some advice what materials to use.
Why not try electrophoretic deposition? You would know the average thickness based on the statistics from engineering specs/data for whatever deposited material. You would also be able to calculate the added volume from Archimedes' principle. You also know the mass density so you could then calculate the surface area of the deposited film/material.
Dip the rock into motor oil. Take it out and and let it drip dry for about a hour. Then place the rock into a container filled with water. For the next few days occasionally move the rock around in the water with the objective of removing the oil from the rock. The area of oil slick on the water’s surface will match the surface area of the rock. If needed you can maneuver the slick into a geometric shaped that can easily be measured.
I think it can work this way also .........use a fast-drying paint bottle to sprinkle the rock...1. measure the rock volume (Archimede law)...2....measure the 'shortest' distance between two selected points on oposite sides of the rock by a caliper 3. spray the rock uniformly(or just use a paintbrush)....4...measure the new distance between same two selected points of the rock...5. ...measure the new rock volume... ---step 4 gives you indirectly how much tickness the paint layer has because you must subtract the new distance from the old one and divide with number 2.... ---step 5 gives you how much volume the paint layer has which you get from subtracting the old rock volume from the new rock volume... Now procede to step 6. which is an arithmetic job of dividing volume of the paint layer by its tickness to get the area of the paint that is approximately the area of the rock....
Depends on the tools you have at your disposal; I'll describe an expensive and inexpensive approach:
The underlying idea's the same: we map 1D slices of the rock onto a 2D surface to model its 3D shape, then obtain a surface area estimate. With the 'expensive' option, this mapping is very granular and precise - with latter, it's as good as your balloon and your wrapping procedure (how it covers bumps, ridges, whether there are empty gaps, etc) - but won't compete with a scan.
Peterh is correct that the task is ill-defined, while the various suggestions offer ways to measure it that define what is being measured and then calculate that measurement to various degrees of accuracy. However I would say that all of the offered definitions of measurement are highly arbitrary; what you really want is a method that is, in some sense, a natural meaning for surface area.
I suggest to you that a natural definition of surface area is the area through which heat is lost since this represents a real and well defined physical property of the object.
The rate of heat loss of a body is proportional to this surface area; therefore in order to calculate the surface area of your rock, what you need to do is raise its temperature to a known value and then calculate how long it takes for the rock to lose temperature. From this measurement you can calculate how fast the rock is losing heat energy. To convert that into an actual surface area you will need to understand the thermal properties of the rock, and so will either need a sample of similar rock or need to sacrifice a proportion of the rock for testing.
Use Nuclear Magnetic Resonance imaging to calculate the position of every atom in the rock. Then count how many atoms border an empty space that is connected to the space outside the rock.
