Where does the photon orbital angular momentum go in light-matter interactions?

Question

Just as a photon's polarization determines its spin angular momentum (or more accurately its helicity), its wavefront can carry orbital angular momentum (OAM) much like an electron in an atom.

Following this Phys.SE question, Selection rules for atomic emission: why doesn't the photon carry orbital angular momentum, it is clear that since atoms are so small (<0.1 nm), they don't really "feel" the OAM of light. This is because the wavefront of optical light carrying OAM changes on the scale of many hundreds of nanometers for optical light, much larger than the atom. Thus, the atom shouldn't really be able to tell the difference between an optical photon carrying non-zero OAM and one with zero OAM.

The logic of the above question is quite sensible in my opinion, but the issue I am having is: where does the OAM go when an atom happens to absorb a photon with non-zero OAM?

I would assume that OAM is conserved in the absorption of the photon and goes into center-of-mass atomic OAM, but is that necessarily true? And how do we reconcile the atom's photon-acquired OAM with the fact that the field is locally identical to an ordinary photon with zero OAM on the length-scale of atoms?

Edit: I want to emphasize that I am only considering optical (visible) light, which is much larger in wavelength than the atom. Additionally, I am thinking of the general case of an atom not located precisely in the central vortex of the OAM beam, but on one of its side lobes.

Answer 1

After reviewing the comments I believe KF Gauss is correct in their statement that the atom picks ups angular momentum with respect to the light propagation axis. See Eq. 5.448 in Quantum and Atom Optics by Steck regarding the mechanical force on an atom by an optical field.

$$ \langle \boldsymbol{F}\rangle = \frac{i\hbar|\Omega(\boldsymbol{r})|^2}{4\left(\frac{\Gamma}{2} - i \Delta\right)(1+s(\boldsymbol{r}))}\left(\nabla \log\left(|\Omega(\boldsymbol{r})|\right) - i \nabla \phi(\boldsymbol{r}) \right) + c.c. $$

Here $\Omega(\boldsymbol{r}) = |\Omega(\boldsymbol{r})|e^{i\phi(\boldsymbol{r})}$ is the complex spatially dependent Rabi frequency. The square magnitude is proportional to the local field intensity as well as some atomic structure parameters and the phase is the phase of the optical field. $\Gamma$ is the atomic spontaneous emission decay rate from whatever excited states are considered for the atomic transition, a two-level approximation is appropriate so that $\Gamma$ is decay from the excited state. $\Delta$ is the detuning between the light field and the atomic transition under consideration. $s(\boldsymbol{r})$ is the atomic transition saturation parameter.

$$ s(\boldsymbol{r}) = \frac{|\Omega(\boldsymbol{r})|^2}{2\left[\left(\frac{\Gamma}{2}\right)^2 + \Delta^2\right]} $$

The first term is the dipole force which says that there is a force proportional to gradient of the intensity of the field. The second term is the radiation pressure force which is a force proportional to the gradient of the phase of the optical field.

Because the phase of an optical field with orbital angular momentum wraps azimuthally (at least away from the center), an atom place in the region of high intensity would feel an azimuthal force, thus impartin orbital angular momentum to the atom.

Note that the formula for the force above is derived from the optical Bloch equations including spontaneous emission. Thus the force arises as a result of the atom absorbing light and spontaneously emitting it in a random direction. I bring this up because it's not entirely obvious to me what would happen if we considered absorption alone.

Answer 2

This is going to be a bit of a half baked answer but here it is.

The usual picture for light with orbital angular momentum is light in a Laguerre-Gaussian Mode mode with non-zero azimuthal index. This sort of field has phase wrapping azimuthally around the propagation axis.

We suppose without loss of generality that the atom is on the propagation axis of the beam*

As I point out in the linked post and as you emphasize in the question, typically when we think about interactions between atoms and light we work in the dipole approximation meaning we assume the electric field is homogeneous across the whole volume of the atom. In the case of light with angular momentum we can see this is not the case. Consider the simplest Laguerre-Gaussian mode with a non-zero phase wrapping.

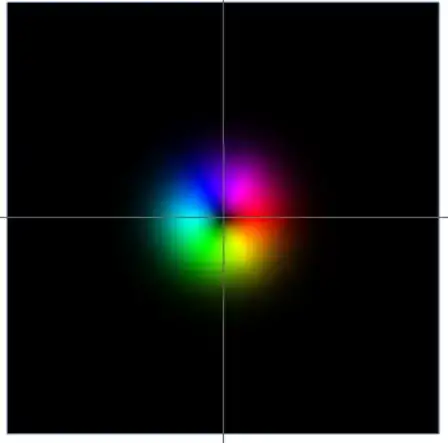
If the atom is in the center of this picture we can clearly see that the dipole approximation is NOT satisfied. This is because the phase of light on the right half of the atom is opposite to the on the left side of the atom. This means no matter what we do with, for example, the scaling of the beam, the atom will never be experiencing a homogeneous field. This means the dipole approximation fails.

When the dipole approximation fails all of the "usual" selection rules that you learn in intro classes are thrown out the window and you need to use higher order selection rules.

I don't know enough about all the details of these selections rules but you can see that this pattern could impart angular momentum to the electron around the nucleus.

And that is my answer to your question. Just like how spin angular momentum of light imparts angular momentum to the electron (atomic "internal" angular momentum) orbital angular momentum of light also imparts momentum to the angular momentum of the electron.

Note that you state

it is clear that since atoms are so small (<0.1 nm), they don't really "feel" the OAM of light.

And you drew this conclusion from my answer to the other question. This conclusion is incorrect. It is possible to have optical fields which vary on atomic length scales (Like the one I have shown above). It just requires using tightly focused or very high order optical fields which need to be carefully aligned so that their regions of large gradients are overlapped with the atom. For example, if the Laguerre-Gaussian mode depicted above is made to be a large beam (waist of a few mm for example) and is offset so that the atom is like in the middle of the red part then the field will look homogeneous to the atom. It is only when the atom is at the central vortex that it strongly experiences the field inhomogeneity.

All of that said you may be interested in Spin-orbital-angular-momentum coupled Bose-Einstein condensates. Note that here the light is not coupled to a single atom but rather to a quantum gas of many atoms in the BEC state. In this case the orbital angular momentum of the light is transferred into the orbital angular momentum of the BEC.

*We can always choose a basis for the optical field which is centered on the atom. If beam is displaced from the atom then in this particular basis it will be composed of a large number of high order modes.

Answer 3

The key to understanding how orbital angular momentum (OAM) can be conserved when a photon that carries OAM is absorbed by a small particle is to understand OAM itself a little better. Note that OAM in a paraxial light beam is always defined with respect to the propagation axis of that beam. If one would pick some random axis pointing in some random direction and displaced away from the beam by some random distance, then the OAM would be different. This is because the linear momentum of the beam now contributes significantly to that amount.

Now back to the particle that absorbs a photon with OAM. As you pointed out, the probability for such an absorption is very small, on the order of $$ \text{probability}=\left(\frac{d}{\lambda}\right)^{2\ell} , $$ where $d$ is the size of the particle and $\ell$ is the topological charge of the optical mode (an integer proportional to the OAM). However, this expression assumes that the particle sits in the centre of the beam, at the vortex, where the light would have been able to apply some torque on the particle. However, the intensity of the light is almost zero. That's why the probability for absorption is so small. It also assumed the mechanism for the absorption is govern by the dipole moment of the particle. If the quadrupole moment is involved, the probability for absorption is proportional to the gradient of the optical field and thus becomes much larger.

But what if the particle sits off-axis in the beam? The probability for absorption (via the dipole moment) becomes much larger, because the light intensity is much larger. This time, there is no vortex that can apply a torque to the particle. So what happens to the OAM? This is where the picture of the linear momentum that I explained before becomes important. The particle would pick up a linear momentum from the photon. In this region, the wave front of the optical field is tilted. So the local propagation vector that optical field has in this region would give the particle a linear momentum that has a slight transverse component. It would be projected along a straight path that is twisted with respect to the propagation axis of the optical beam. When one computes the OAM due to this linear momentum with respect to the original propagation axis of the optical beam, one finds that it gives exactly the amount of OAM that was carried by the photon that was absorbed.

Answer 4

You’ve posed a profound and significant question. In a circularly-polarized paraxial OAM beam, the photons possess a total angular momentum of $(\pm 1+l)\hbar$ along the propagation axis. Here, $l$ is an integer denoting the topological charge of the OAM beam. The first term, $\pm\hbar$, is attributed to the inherent polarization (helicity or spin) of the photon, while the second term arises from what is classically described as the photon’s helical motion around the propagation axis due to the helicity of the wavefront. When a photon of this nature interacts with an atom (in the dipole approximation), its absorption process follows the standard dipole-allowed selection rules that also apply to non-OAM photons. This implies that only the $\pm\hbar$ component of the angular momentum is relevant for the absorption or emission process. If the photon is absorbed by the atom, the $l\hbar$ component is added to the orbital angular momentum of the atom’s center-of-mass (CM) along the propagation axis (regardless of the position of the atom from the propagation axis). Hope this helps.

Answer 5

You’ve posed a profound and significant question. In a paraxial OAM beam, the photons possess a total angular momentum of $(\pm 1+l)\hbar$ along the axis of propagation. Here, $l>0$ denotes the topological charge of the OAM beam. The first term, $\pm\hbar$, is attributed to the inherent polarization of the photon, while the second term arises from what is classically described as the photon’s helical motion around the propagation axis. When a photon of this nature interacts with an atom, its absorption process follows the standard one-photon absorption selection rules that also apply to non-OAM photons. This implies that only the $\pm\hbar$ component of the angular momentum is relevant for the absorption process. If the photon is absorbed by the atom, the $l\hbar$ component is added to the orbital angular momentum of the atom’s center-of-mass (CM) along the propagation axis. Hope this helps.

Answer 6

where does the OAM go when an atom happens to absorb a photon with non-zero OAM

It is simple : the photon can raise an electron to a higher energy level only if all the quantum numbers are conserved,including angular momentum. It is not enough to have the energy difference ( within the width of the energy level).

If the photon is head on with the atom, its trajectory passes through the center of mass, it will have zero angular momentum, which is the usual visualization of exciting energy levels. If its angular momentum is close (within the width of the level) to an integer number of h_bar, and an energy level exists that can absorb its energy ( within the width) the photon will be absorbed, other wise it will scatter off. The atom will be at the appropriate l, so the photon's angular momentum becomes the atom's, ( until the atom de-excites the electron falling to a lower energy level)