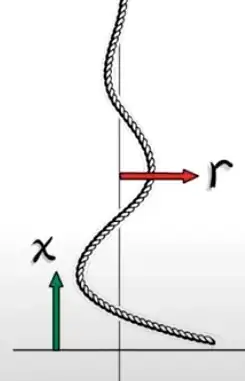
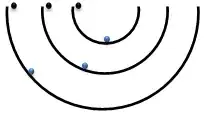
I have always been interested in why objects like chains, ropes, etc. move the way they do when "rotated" around a vertical axis while being held only where it is suspended. It forms a shape if you will, resemblant of a "C" or a wave depending on the length. I am curious to know what laws and effects of physics are at play.
Not a real answer but I'd like to note the model used while studying these phenomena. The shape of rotating chains is modeled by the Bessel functions. Precisely speaking, the radial displacement function $x$ is given as:
$$ r(x) = J_o ( \frac{2 \omega \sqrt{x}}{\sqrt{g}})$$
Where, $\omega_o$ is the angular frequency at which rope is spun, $g$ is gravitational constant and $x$ is the distance from the bottom of the chain
Where,
$$J_o(x) = \sum_{k=0}^{\infty} (-1)^k \frac{x^{2k}}{(k!)^2}$$
A better presentation is done by professor Ghrist in this video
I think it is hard to study your problem, however, I try to justify why a chain/rope hanging from the ceiling makes a $C$ shape as it dangles freely. For a better perception, simulate each ring of the chain as a separate tiny ball which tends to move on a circular frictionless surface. Due to different radii of these surfaces, the period of oscillation would be different for each of the balls. $(T\approx 2\pi \sqrt{r/g})$ That is, the farther balls need more time to reach the lower part of their assigned circles because farther surfaces have greater radii. This difference in periods causes the distant balls (rings of the chain) from the center (pivot) to lag behind the nearer ones making a C shape.
If i understand correctly you spin the chain on an vertical axis with angular speed $w$. The 3-dimensional shape of the spinning chain is rather complex, but a 2-dimensional projection of this shape on a vertical plane resembles a standing wave. Where the nodes are the points where the chain is kept in the middle. If you increase the length of the chain you will have to adjust the angular speed, but more nodes will appear. And i guess that these nodes have the same relation with the length of the chain and $w$ as a simple 2-dimensional standing wave
