Normal force on a particle residing on a cone apex

Question

By reading Norton dome "proof" about non-determinism of Newton laws, i've started to think about how much Norton system is physical at all. Let's push it to the limits. Let's say we have vertical cone and a particle sitting exactly on cone apex :

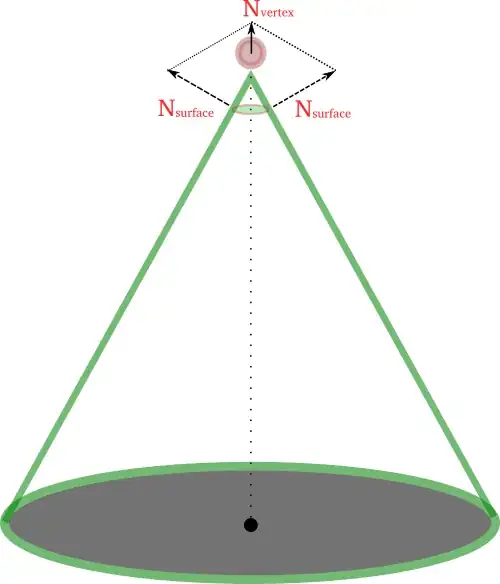
Usually normal force is defined as normal vector perpendicular to surface where body is placed. However, here body-particle is placed not on surface at all, but just at cone apex, meaning that it's just a singular point. So, surface normal will not help here. Best bet is to calculate vertex normal which can be defined as averaging all surface normals at some cone cross-section :

$$ \hat{\textbf{n}}_{vertex} = \frac{\sum_{i}{\vec{N}_{surface_{_i}}}}{||\sum_{i}{\vec{N}_{surface_{_i}}}||} $$

So we have got a unit vertex normal vector. This is perfectly valid in mathematical sense and used a lot in computer graphics too. But, the question is - Is it physically meaningful to use vertex normal here as a unit normal force vector (substitute for SURFACE normal force) ?

Answer 1

Apex normal force is undefined.

Proof 1

Considering this schematics :

Surface normal approaching top from the left of $x$ axis is not equal to surface normal approaching top from the right at some cross-section of cone going through main $z$ axis , i.e. $$\mathbf n_{top}^+ \ne \mathbf n_{top}^-$$

and since by definition this is a jump discontinuity,- normal force is undefined, since it's a scaled surface normal, i.e. $\mathbf N = a \mathbf n$ (if surface normal is undefined, then normal force too).

Proof 2

Surface normal of elementary area is defined as, $$ \mathbf n = \frac{\mathbf p\times \mathbf q}{dA} ,$$ where $\vec p,\vec q$ are some perpendicular vectors along elementary area edges. So, since at the top elementary area vanishes (point area is zero), we get $$ \vec n_{~top} =\frac {\vec 0 \times \vec 0}{0} $$ which is indetermine form and so normal force at the top is undefined.