This is certainly a semantic question, but I will say that I have both heard and used the term "dangerously irrelevant" in both of those contexts as well as others where your vague initial definition fit. So far I haven't had anyone get angry at me, so I suppose that is a good sign. I'd definitely be interested in hearing about the history of the term (I think I've seen it used as early as the mid-70s to describe your first bullet point, but Wikipedia seems to prefer the second definition).
Regarding your main question, I would say that your two bullet points are distinct phenomena, because they really involve distinct behavior of the irrelevant operator. I'd concretely describe your bullet #1 definition as an operator which is irrelevant at some unstable fixed point FP, but relevant at one of the fixed points which lie in a relevant direction from FP, call it FPR. Thus, after a small but finite tuning away from your FP in the relevant direction, the operator will initially flow towards zero, but as the theory flows towards FPR, its flow towards zero will stop and it will begin to grow again.
There is a really nice discussion of this in Chubukov, Sachdev, Ye:
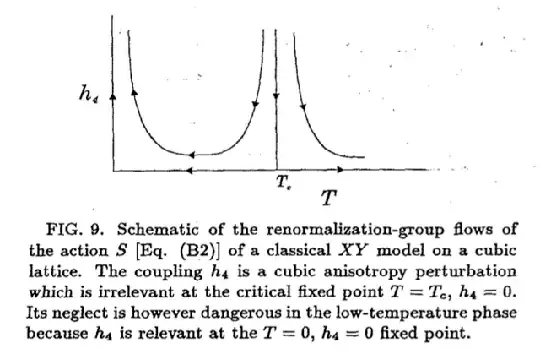
This image is taken from Appendix B, which is partially a very nice review of dangerously irrelevant operators as per your first definition. They are considering a classical 3D XY model in the presence of a ("dangerously irrelevant") term $h_4$ which breaks the O(2) symmetry down to $\mathbb{Z}_4$.
As you say, if you discard the irrelevant operator at $T_c$ you lose information about the fixed point you end up at. I think a really crucial aspect of this scenario is the presence of two large length scales near the phase transition: for small $(1 - T/T_c)$, as you increase the length scale you are probing, you first see a crossover from critical to Goldstone fluctuations on the order of a length scale $\xi_J$, and then you see a crossover to a "gapped" theory with $\mathbb{Z}_4$ order on a much larger length scale $\xi_4$. This allowed the authors to actually ignore this "dangerous irrelevance" for essentially the entirety of the main text of their paper. (In fact that paper missed that there is another dangerously irrelevant operator which alters the applications in the main text to certain antiferromagnets, but that's a long unrelated story.)
The usual example for your second bullet point is the dangerous irrelevance of interactions for $\phi^4$ theory in $D\geq4$. But in this case, it's referring to a failure to even take the scaling limit in a finite neighborhood of the critical point. Say you have a relevant coupling $t$ and irrelevant coupling $u$; you would like to describe the physics in terms of some scaling functions
$$
f(t - t_c,u - u_c).
$$
For your first definition, there is nothing wrong with setting $u = u_c$, and you will obtain a nice scaling function describing the singularities as a function of small $t - t_c$, and it will even be accurate to "large" (but not too large) length scales. But for $\phi^4$ theory in $D\geq 4$, you encounter new singularities by tuning $u \rightarrow u_c$. You're forced to consider $u > u_c$ even though it is properly irrelevant in both nearby phases and is always "trying" to flow to $u_c$, so one doesn't see the emergence of a new length scale ($u$ just weakly renormalizes the existing length scales). To me, it really seems qualitatively different from the first definition.
I'll add that even in scenarios different from your two definitions, I have referred to observables which depend sensitively on corrections to scaling as "dangerously irrelevant observables." I'm not sure if this usage would be considered offensive to anyone.
