I have the following diagram (velocities are relative to p2):
and I have the following line of reasoning:
But this reasoning means that when P1 reaches P2, it has not yet reaches P3 which seems incorrect. Can someone explain where my reasoning breaks?
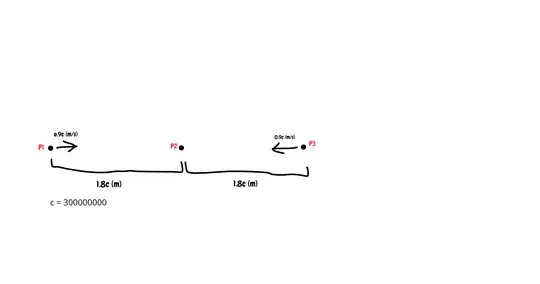
You basicaly forgot time dilatation, length contraction and relativity of simultaneity.
Since the diagram is drown in the P2 system, it takes 2 seconds for both light signals to reach P2 in this system.
When you transform to P1, the speed of P2 is indeed 0,9c, but now the length is contracted by lorentz factor $\gamma$, so the distance in P1 frame is $1.8c*\gamma$. So it takes $t_1=2\gamma$ seconds for P2 to reach P1. Note that this is ok, since the times passed in P1 and P2 reference frames are dilated exactly by the factor $\gamma$ so transforming the time back to P2 reference frame gives you again 2 seconds.
And for the P3:
The speed in the P1 reference frame is $v_3=1.8 c/1.81 $ and the distance is $l_{13}=3.6c*\gamma$ in the P1 system. Thus, the P3 signal will reach point P1 in $3.62\gamma$ of P1s time. The difference $1.62\gamma$ seconds is "lost" in the relativity of simultaneity.
For P2 system the events P1 started moving toward P2 and P3 started moving toward P2 are simultaneous. Then you assumed in P1 system the events P2 started to move toward P1 and P3 started to move toward P1 are simultaneous. That is not so. From the P1s point of view, when P3 started to move toward P1, the P2 was still "waiting" to start moving.
How long it did wait is given by the formula $${\displaystyle \Delta t'=\gamma {\frac {-v\,\Delta x}{c^{2}}}}$$ for comparing the time passed in primed reference frame (moving with velocity $v$ with respect to unprimed system) between two events, that are simultaneous in unprimed frame with space separation of $\Delta x$. For you example (i.e. between events P2 started moving and P3 started moving) that would be $0.9*1.8\gamma=1.62\gamma$ seconds as it should.
