1

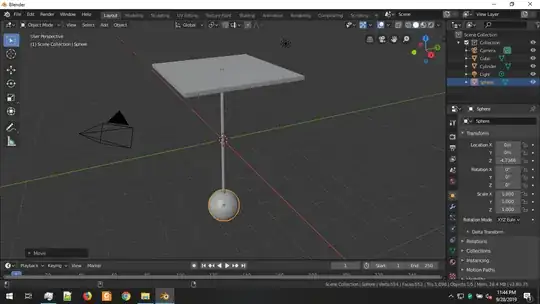
I have I have some objects assembled like this :

enter image description here

The inertia tensor would be :

$$I=I_1+I_2+I_3-m_1 \,\tilde{r}_{01}\,\tilde{r}_{01}-m_3\,\,\tilde{r}_{03}\,\tilde{r}_{03}$$

Where :

$$\tilde{r}_{01}=\begin{bmatrix} 0 & -z & 0 \\ z & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}$$

and $$\tilde{r}_{03}=\begin{bmatrix} 0 & +z & 0 \\ -z & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}$$

According to this.

Detailed notations here.

But what is the inertia if -

  • I rotate the planar object on the very top(everything with it) around $Z$-axis
  • Just rotate the rod and sphere (except the planar object), just like a pendulum. Let angle with $X$-axis is $\alpha$ and angle with $Y$-axis is $\beta$
  • Do both together
Maifee Ul Asad
  • 187

1 Answers1

3

The inertia tensor obeys the congruent transformation from the local coordinates to the world coordinates.

If you have a 3×3 rotation matrix $\mathbf{R}$ then you have

$$ \mathbf{I}_{\rm world} = \mathbf{R} \, \mathbf{I}_{\rm body} \mathbf{R}^\top $$

So the combined inertia would be

$$ \mathbf{I} = \mathbf{R} \, \left(\mathbf{I}_1 +\mathbf{I}_2 + \mathbf{I}_3 \right) \mathbf{R}^\top - m_1 \overline{\boldsymbol{r}}_1 \overline{\boldsymbol{r}}_1 - m_3 \overline{\boldsymbol{r}}_3 \overline{\boldsymbol{r}}_3$$

You must make sure the vectors $\boldsymbol{r}_n$ point to the center of mass in the world coordinate system after the body is rotated.

See also this answer to a similar question.

John Alexiou
  • 40,139