I am having a tough time visualizing the derivation of boundary conditions in Electrostatics. My main problem lies with the fact $\oint \mathbf E\cdot \text d\mathbf l = 0$ is used instead of $\oint \mathbf D\cdot \text d\mathbf l = 0$.
So my question is what will be the best example and also a formal proof to show the former relation holds true while the second one is not true?
The definition of $\mathbf D$ is $$\mathbf D=\epsilon_0\mathbf E+\mathbf P$$ where $\mathbf P$ is the polarization vector that is due to bound charges in your material, i.e. $\nabla\cdot\mathbf P=-\rho_B$
Since $\nabla\times\mathbf E=0$, it must be that $$\nabla\times\mathbf D=\nabla\times\mathbf P$$
And here is the issue. We are not guaranteed to have $\nabla\times\mathbf P=0$ so that the $\mathbf D$ field has zero curl. If $\mathbf D$ has a non-zero curl, then it cannot be true that $\oint\mathbf D\cdot\text d\mathbf l=0$ for all closed paths. This is why you do not see this condition used. It is not always true.
Griffiths makes the following argument in his book.
Looking first at a point charge at the origin using Coulomb’s Law:
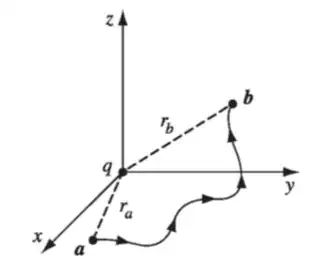
$$ \int_a^b \mathbf{E}\cdot \text d\mathbf{l} = \frac{1}{4\pi\epsilon_0}\left( \frac{q}{r_a} - \frac{q}{r_b}\right)$$
That equals zero when $r_a$ = $r_b$. Then combining that result (given the fact that it holds true for any reference point not just the origin) with the principle of superposition, you could prove that it holds true for any charge distribution.
So even though you can talk about the divergence of D in terms of free charge, there is still no Coulomb’s Law type equation relating it to free charge so this integral doesn’t necessarily hold:
$$ \int_a^b \mathbf{D}\cdot \text d\mathbf{l} \ne \frac{1}{4\pi\epsilon_0}\left( \frac{q_f}{r_a} - \frac{q_f}{r_b}\right)$$
