2

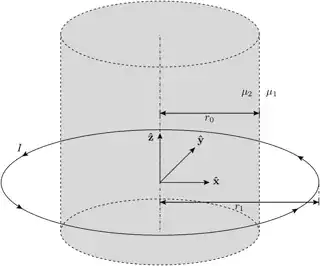
I am trying to determine if the following problem has an analytical solution using the method of images. The problem is an infinitely long (in $z$) cylinder of a material with permeability $\mu_2$ of radius $r_0$, where the region outside the cylinder has permeability $\mu_1$. In the latter region there is a ring of constant current $I$ of negligible thickness, and with radius $r_1 > r_0$. This situation is illustrated in the following diagram:

enter image description here

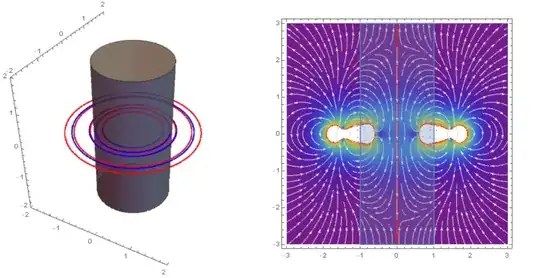
The question is whether the method of images could be used to place image rings of current to solve for the fields in either region. I've done a little investigation into this question and this is leading me to believe that no simple configuration of image rings can meet the necessary boundary conditions at the region interface. This is after seeing this similar question and also after working with the equations in this paper for the magnetic field from a ring of current. So does anyone know for sure whether this can be solved using the method of images or not?

Note that the analogous electrostatics problem (I think) is a ring of charge around a cylindrical region of different permittivity or a perfect conductor.

Urb
  • 2,724
kyp4
  • 71

1 Answers1

1

For definiteness, we put $\mu _1=1,\mu _2=200, r_0=1,r_1=1.5$. Then this problem of constructing images of a ring in a cylinder with high magnetic permeability can be reduced to the optimization problem. As an exact solution for a current loop, we use equations (24) and (25) from the article Simple Analytic Expressions for the Magnetic Field of a Circular Current Loop describing the radial and axial component of the magnetic field induction in the form $$B_{\rho}=B_{\rho}(r_i,\rho,z),B_z=B_z(r_i,\rho,z) $$ We assume that the magnetic field of such a system can be described as a superposition of the field of the original loop and all its images in the form $$B_{\rho}=\sum_{i=1}^n {c_iB_{\rho}(r_i,\rho,z)},B_z=\sum_{i=1}^n{c_iB_z(r_i,\rho,z)} $$ Here, the parameters $c_i, r_i$ can be found by optimizing the functional minimizing the residual of boundary conditions on the surface of the cylinder $$f=\sum_{j=1}^m{[B_{\rho}(r_0-\epsilon,z_j)-B_{\rho}(r_0+\epsilon,z_j)]^2+[B_z(r_0-\epsilon,z_j)/\mu_2-B_z(r_0+\epsilon,z_j)/\mu_1]^2}$$ One example of successful optimization with $n=11,m=41,\epsilon=1/15$ leads to $f=0.0000208766$ and $c_1= -1.06691, c_2= 0.963961, c_3= -1.06325, c_4= 0.994663, c_5= -1.05188, c_6= 0.974633, c_7 = -1.02329, c_8= 0.987478, c_9= -1.38852, c_{10}= 0.659527,c_{11}=1, r_1= 0.780427, r_2= 0.763184, r_3= 0.780421, r_4= 0.763187, r_5= 0.961497, r_6= 0.933601, r_7= 1.11224, r_8= 1.09194, r_9 = 1.55361, r_{10}= 1.73244,r_{11}=r_1=1.5$ The general view of the loops and magnetic field is shown in Fig. 1 Figure1

Alex Trounev
  • 3,854