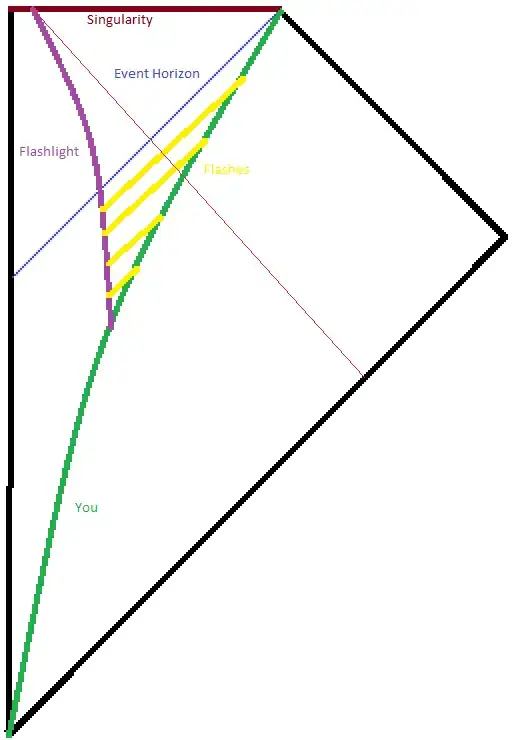
This is my third question from a series were I progressively refine my thought experiment. The others are:
- Can something (again) ever fall through the event horizon?
- Time of flashlight crossing the event horizon as seen from an external observer
Assume I am stationary over a Schwarzschild black hole of mass $M$. Some force is keeping me at a distance $d$ over the event horizon (or the black hole center, whatever is easier to answer). At time $0$ I drop a flashlight blinking at frequency $f$ into the black hole. At what time $T_{M, d}(f)$, in my own frame of reference, will I see the last blink of the flashlight?
Some assumptions (non-comprehensive list):
- Assume only general relativity (the world is not quantized, no Hawking radiation);
- The flashlight is not destroyed/spaghettified by the tidal forces;
- I can always detect the flashlight as long as it has not crossed the event horizon;
- I can set $f$ to any arbitrarily big frequency.
It would be nice if the answer was the actual function/algorithm describing $T_{M, d}(f)$, so I could graph for increasing values of $f$, but the real information I want to know is:
Is it true that $$\lim_{f \rightarrow \infty} T_{M, d}(f) = \infty \;\;\;\; \text{?}$$