0

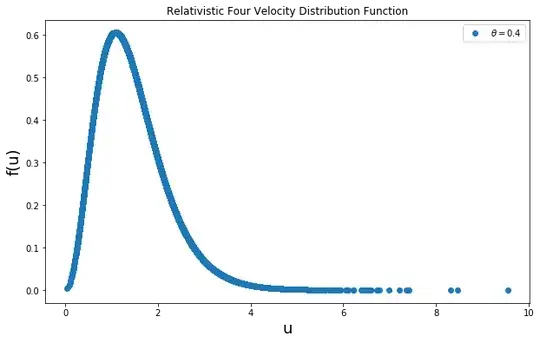
I am trying to sample Maxwell-Jüttner distribution using the Sobol method as described in Zenitani Loading relativistic Maxwell distributions in particle simulations (2015). Equation (2) in the paper assumes $m=c=1$ and then goes on to describe how to sample the four-velocity. I have a few questions regarding the Sobol algorithm:

  1. If $m$ and $c$, are not taken to be unity, how will that affect the value of generated $u$? I can see how this will affect $f(u)$, but does $u$ also need to be scaled?
  2. In order to get $v$, which the normal three velocity vector, do we just need to use the relation $u = \gamma v$, and express $v$ in terms of $u$?

I am attaching my distribution plot for reference.

enter image description here

Prav001
  • 142

1 Answers1

1

OP's equations are \begin{align} f(\mathbf{u})\,\mathrm{d}^3u&=\frac{N}{4\pi m^2cTK_2(mc^2/T)}\exp\left(-\frac{\gamma mc^2}{T}\right)\,\mathrm{d}^3u\tag{1} \\ \Rightarrow f(u)\,\mathrm{d}u&=\frac{N}{TK_2(1/T)}\exp\left(-\frac{\sqrt{1+u^2}}{T}\right)u^2\,\mathrm{d}u\tag{2} \end{align} where $\mathbf{u}=\gamma\mathbf{v}$ is the spatial components of the 4-velocity, $\gamma$ the Lorentz factor, $N=\int f(\mathbf{u})\,\mathrm{d}u$ is the total number density, $T$ the temperature and $K_2(x)$ the modified Bessel function. The $4\pi$ factor is dropped in (2) due to use of spherical coordinates and it is plain to see that, $$ u=\gamma v\implies \gamma=\sqrt{1+u^2/c^2} $$

Since $u$ is the velocity, then $m\neq1$ should be straight-forward re-insertion. Additionally, since $u=\gamma v$, then there should be no changes to $u$, only to $f(u)$. Lastly, indeed you should invert the relation between $u$ and $v$ to get the 3-velocity, though the work is done for you in Zenitani's paper (and above): $$ v_i=\frac{u_i}{\gamma}=u_i\cdot\left(1+u_i u^i\right)^{-1/2} $$

In my opinion, it may not be the best of ideas to not use $c=1$, since using such scaling is intended for convenience (in both notation and in coding) in relativistic settings. Since the Maxwell-Jüttner distribution describes the relativistic distribution of velocities, it probably would be better to stick with $c=1$.

Kyle Kanos
  • 29,127