Physical significance of the decomposition $3\otimes\overline{3}=8\oplus 1$ in meson classification

Question

Under the assumption of $SU(3)$ flavour symmetry of early days, proposed by Gell-Mann and Neeman, among other irreducible representations, the meson octet was obtained. This result from the $SU(3)$ decomposition: $$\:\boldsymbol{3}\boldsymbol{\otimes}\overline{\boldsymbol{3}}=\boldsymbol{8}\boldsymbol{\oplus}\boldsymbol{1}\:$$ This decomposition tells that eight bound states belong to the irreducible octet representation and one state belongs to the singlet. In what way these eights states are to be distinguished from the singlet state?

Answer 1

Take a look at the pseudoscalar mesons, a well understood family, since they comprise the pseudogoldstone bosons of spontaneous chiral symmetry breaking in 3 light flavor QCD.

Flavor SU(3) arranges the octet in this pattern,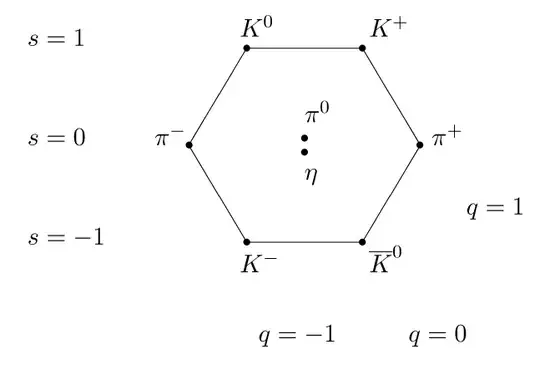

and the singlet is $\eta'$, off the picture, since it has no isospin or strangeness, so U or V spin, to have any of its properties connected with those of the particles in the octet by the symmetry: it's on its own. (η in the center of the octet is an isosinglet, but connects to the rest via U,V spin!) You might as well think of it on a separate planet...

A celebrated, quick consequence of this isolation is that it picks up its mass through a recondite topological property of the QCD vacuum (gluonic nonperturbative interactions): even though it looks as though it is made up of the same quarks as the $\eta$ and the $\pi$, its mass is huge (958MeV), compared to those of the $\eta$ (548MeV) and the $\pi$ (135MeV), and even the strange Ks (498MeV).

Moreover, the singlet $\eta'$ cannot use any of the (then!) astounding SU(3) mutual correlations of the octet members' properties, masses and couplings to other mesons and baryons that Gell-Mann & Ne'eman observed early on in 1961-2.

Answer 2

I'm not quite sure if I've got you right on this but let me try with a concrete example instead of a more general and abstract answer. I assume that you are familiar with gluons and color charge. The members of the octet each carries a color and an anti-color.

1. $r\bar{g}$
2. $r\bar{b}$
3. $g\bar{r}$
4. $g\bar{b}$
5. $b\bar{r}$
6. $b\bar{g}$
7. $\frac{1}{\sqrt{2}}\left(r\bar{r}-g\bar{g}\right)$
8. $\frac{1}{\sqrt{6}}\left(r\bar{r}+g\bar{g}-2b\bar{b}\right)$

The members of the singlet do not carry any net color.

1. $\frac{1}{\sqrt{3}}\left(r\bar{r}+g\bar{g}+b\bar{b}\right)$

This is one way to distinguish them. I hope this helps. Otherwise you could skim through the following document for a more in-depth explanation: Quantum Cromo Dynamics - Lecture Notes