One statement I've heard many times is that QFT is "defined" by the lattice, or that the "only" definition of QFT is on the lattice (when such definition exists, e.g in pure Yang-Mills theory). I've heard that from many people I respect, but I have my doubts. Specifically - the lattice is an algorithmic definition of those quantities that can be calculated in Euclidean spacetime. As I said in my answer to this question, this is a proper subset of all physical quantities you may be interested in calculating in general, and many physical situations do not have Euclidean formulation. Is there some response to this objection I am missing, or am I being naive somehow?
5 Answers
I can only guess that "QFT is defined on the/a lattice" means that certain infinities in Lagrangian QFT come from defining QFT on a smooth (Lorentzian or Euclidiean) manifold, while many physicists suspect that the "smoothness" is an approximation that breaks down on a certain length scale (like the Planck length), and incorporating the true - quantum - nature of spacetime will cure the QFT-infinities. In this sense, defining QFT on a lattice is a better approximation than defining QFT on a smooth manifold.
I would object, however, that there is no single, unifying framework for doing QFT, Lagrangian QFT is only one approach. There is of course algebraic/local/axiomatic QFT that does not have any problems to define QFTs on globally hyperbolic Lorentzian manifolds at all - it does have a problem with the construction of interesting models, but in the last two decades there has been some progress.
There has been one specific approach that elevates operator product expansions to a defining property, an axiom, of QFT, it started somewhen around this paper:
- S. Hollands, R. M. Wald: Quantum field theory in curved spacetime, the operator product expansion, and dark energy
An introduction and a toy example can be found in this thesis:
This is a very new approach, which I cite mainly to illustrate that there is a lot of room left for the development of an unifying, axiomatic approach to QFT which, when found, may change our thinking about QFT significantly.
(I'm also aware of the fact that many people in quantum gravity think that everything about QFT is said and done: well, shoot me.)
- 3,755
Moshe, I hope others will give their answer and I would also like to read it.
But I agree with you that the Euclidean calculations are "only" good for some rather important quantities that are easy to be calculated in the Euclidean setup - and they should be continued to the Minkowski spacetime. Some time-dependent questions surely make it more natural to try to solve things directly in the Minkowski spacetime. However, the full set of on-shell scattering amplitudes or off-shell Green's functions is a very important set of observables and, in some sense, contains "all the dynamical knowledge" about the theory. And this dynamical knowledge is much more naturally calculated in the Euclidean setup which is why people like me wouldn't be afraid to say that the Euclidean calculations are more fundamental.
Somewhat independently of that, there's the question of lattice QFT. Lattice QCD is usually meant to denote the Monte Carlo calculations etc. and they're calculated in the Euclidean spacetime. However, you may also discretize the spatial coordinates only, do the Hamiltonian lattice QCD, and keep the Minkowski space. I would separate the Euclidean spacetime from the latticization as two different and largely independent procedures.
Discretizing spacetime is a straightforward procedure to approximate a real theory if we want to calculate it on a digital computer. Many people think "discretely" and they have a problem to distinguish the reality from the computer models. That's why they think that the discrete models are the "real thing", and lattice QCD is their definition of choice. Of course, there is nothing scientific about this attitude.
Nature has no trouble to work with continuous quantities - and fields that depend on continuous variables (and even infinitely many variables, if necessary) - and even the physicists, who are much more limited than Nature, have learned many mathematical ways that allow them to directly calculate the results in the continuous spacetime.
Needless to say, some properties of the system change when the spacetime is Wick-rotated to the Euclidean one (or back); and when the spacetime is discretized. The first transformation changes the reality conditions for the spinors and produces various problems with the fermions. The second transformation - the discretization - also produces its related problems with the fermions, the fermion doubling problem etc. Moreover, it breaks the continuous translational symmetry, and because the supersymmetry anticommutes to translations, lattices inevitably break (most of) the supercharges, too.
Of course, if one views supersymmetry as a key property of a theory, its loss is a huge problem and mostly invalidates the idea that the lattice definition is "more real" or "more fundamental".
To summarize, the latticization is just one particular way - one of the conceptually simplest or most straightforward ways - to define a theory that flows to the desired quantum field theory at long distances. And some people want to confine their reasoning into the lattice because they believe that their duty as scientists is to behave as similarly to a mindless digital computer as possible. (Even computers may deal with non-lattice approaches, but that requires them and the programmers to learn some serious maths and not just mechanical operations on a lattice.) As far as I know, there is no scientific justification of the idea that the "right" definition of a field theory should ultimately boil down to a lattice.
- 182,599
Lattice QCD is define on a grid with spacing $a$, and where on the edgelinks there are gauge potentials. The reciprocal lattice spacings are momentum cut-offs, and must be set so that the heaviest quark mass is $m_q~>>~1/a$. So the lattice spacing is not entirely arbitrary. A discrete difference in gauge potentials defines the fields $$ F_{ij}~=~(A_j(x’)~-~A_i(x”))~-~(A_i(x”’)~-~A_j(x”’))~-~g(A_j(x’)A_i(x”)~-~A_i(x“’)A_j(x“’)) $$ where the coordinates are illustrated in the figure. The internal gauge indices are implied.
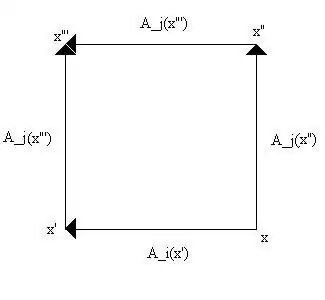
This evaluates the gauge potential around a square or plaquette, which is in a large grid. The field is then evaluated as one evaluates a magnetic field as $B~=~-\nabla\times A$ as evaluated in the area of the plaquette. This means the Lagrangian for the quantum system is periodic, and is similar in some ways to a Bloch potential. The limit that one takes the lattice spacing small enough the funny periodic nature of the Lagrangian due to the lattice plays an insignificant role. This is one reason the inverse lattice spacings have to be smaller than the quark masses.
So the lattice is a finite element approach to QFT, which is set to the cut off scale of the theory. Lattice QCD is worked because the nonlinear nature of the theory makes explicit calaculations exceedingly difficult, particularly due to inverse screening. This make the computation of the hadron spectrum tough where one does not has asymptotic freedom to work with.
- 9,408
Unless someone can show how to come up with chiral fermions and avoid the fermion doubling problem over a lattice, it's clear lattice regularizations can't cover everything. That person would have to bypass the Nielsen-Ninomiya theorem.
- 2,377
As far as I understand, a lattice formulation makes it possible to employ "naturally" the famous Wilson's reasoning about scales and "effective" theories. Factually there is nothing physical in this QFT "definition" since the lattice step is arbitrary unlike in the Wilson approach to the critical phenomena. I would call it a "fog" to hide real physical problems in.
- 14,125