A minimum, if boring example is that of two uncoupled 1D linear ODE (with incommensurate constants) on a torus, such as can be found in Hasselblatt & Katok:
$$\left\{
\begin{aligned}
\dot x &= \omega_1\\
\dot y &= \omega_2,
\end{aligned}
\right. \tag{4.2.3}
$$
whose trivial solution is
$$\left\{
\begin{aligned}
x &= x_0 + \omega_1t\\
y &= y_0 + \omega_2t.
\end{aligned}
\right. \tag{4.2.4}
$$
The simplest nontrivial example I could find is the forced van der Pol oscillator (still simpler than the example of two of them coupled, mentioned in the OP), found, e.g., in Guckenheimer's 1980 paper (e-print):
$$\left\{
\begin{aligned}
\dot x &= y - \epsilon(x^3/3 -x)\\
\dot y &= -x+b\cos(\omega t),
\end{aligned}
\right.
$$
which can be written as an autonomous system in 3D:
$$\left\{
\begin{aligned}
\dot x &= y - \epsilon(x^3/3 -x)\\
\dot y &= -x + b\cos z\\
\dot z &= \omega.
\end{aligned}
\right.
$$
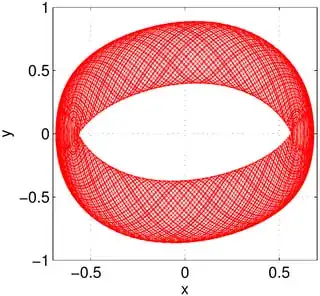
A numerically integrated quasiperiodic trajectory of this system, in normalized variables, can be found in this paper (e-print):