What is the difference between position, displacement, and distance traveled?

Question

Suppose the question is somewhat like this:

If $v=8-4t$ and the position at time $t= 0\ \rm s$ is $2\ \rm m$, find the distance traveled, displacement, and final position at $t=3\ \rm s$

Since $\text dx/\text dt=v=8-4t$, then $\text dx=(8-4t)\text dt$. After integrating we find $x(t)-2=8t-2t^2$, and substituting the value of $t=3\ \rm s$ we get $x(3)=8\ \rm m$.

Is the answer that I found displacement, position or distance?

It can't be distance. I am sure of this. But is it position or displacement?

Answer 1

Position is a single point. Usually in space we indicate positions with coordinates like $(x,y,z)$ in Cartesian coordinates, $(r,\phi,\theta)$ in spherical coordinates, etc. We can also define the position as a vector, i.e. the position vector, that is a vector that points from the origin (subjectively defined) to the position of the particle in question. It could be $\mathbf r=x\hat x+y\hat y+z\hat z$ using Cartesian coordinates, $\mathbf r=r\hat r$ using spherical coordinates$^*$, etc. In 1D there really isn't anything different between the position coordinate and the position vector, so you don't need to worry about the distinction in the problem you have described in your question.

Displacement is the change in position. It is a vector quantity; it is the difference between two position vectors. So, for example, if you go around a circle exactly one time, your displacement over that time is $0$. You can get the displacement at some time $t$ by integrating the instantaneous velocity over time: $$\Delta\mathbf r=\mathbf r(t)-\mathbf r(t_0)=\int_{t_0}^t\mathbf v(\tau)\text d\tau$$ Notice that $\mathbf r(t)$ is the position at time $t$, and $\mathbf r(t_0)$ is the initial position you are calculating the displacement with respect to. Hence the integral gives displacement since it is the difference between the final and initial position vectors.

Distance is a little different, but it is easy to understand. You can think of it as what the odometer in your car gives to you. It just tells you how far you have traveled without reference to some starting point. Going back to the example of going around a circle one time, your displacement was $0$, but the distance you traveled is equal to the circumference of the circle. Distance is a scalar value. You can determine it by integrating the speed over time: $$D(t)=\int_0^t|\mathbf v(\tau)|\text d\tau$$ Note that this integral is the same thing as the curve length of the path the particle moves along (i.e. the distance you have traveled).

These explanations should help you in your own problem.

---

$^*$ Note that the position vector in spherical coordinates is not $\mathbf r=r\hat r+\phi\hat\phi+\theta\hat\theta$. This is because the position vector, by definition, points from the origin to the position (coordinate) of the particle. Therefore, the position vector can only have a radial component, i.e. $\mathbf r=r\hat r$

Answer 2

• $\color{blue}{\text{Position}}$: $$\color{blue}{\vec p(t)}$$

• $\color{red}{\text{Displacement}}$†: $$\color{red}{\vec p(t_2) - \vec p(t_1)}$$

• $\color{green}{\text{Distance Traveled}}$: $$\color{green}{\int_{t_1}^{t_2} \left\|\frac{d\vec p(t)}{dt}\right\|dt}$$

†Displacement is sometimes defined as the scalar $\|\vec p(t_2) - \vec p(t_1)\|$.

Answer 3

What is the difference between position, displacement, and distance traveled?

Succinctly:

(1) the position of an object is a vector with tail at the origin of the coordinate system and head at the location of the object.

(2) the displacement of an object is the vector difference of the current position vector of the object and the position vector of the object at an earlier time. That is, the tail of this displacement vector is at the earlier position and the head is at the current position. The length of this vector is, generally, the shortest distance between the earlier and current positions.

(3) the distance traveled from the earlier position to the current position is not a vector but is, rather, a path length. There are an infinity of paths that an object may take from the earlier position to the current position and, in general, each has a different associated length.

Answer 4

So the 8m is displacement or distance?

The 8m is the position of the particle. The displacement is 6 m.

When you integrated the velocity function to get position you included a constant of integration (2 m) to account for the initial position of the particle, that is, its position at time t=0, which is given as 2 meters. If you omitted the constant of integration then you would be calculating the change in position, i.e. the displacement, and not the position. In this case the displacement would be 6 m.

Position can be considered as a point in a coordinate system relative to the origin of the coordinate system. The diagram below shows the position $s$ of the particle in a one dimensional coordinate system, relative to the origin of the system, s=0. In effect, when the particle's position is 2 m the timer is started, i.e. t=0. Displacement is then distance between two positions of the coordinate system as a function of elapsed time (3 s), which in this case 6 m.

Hope this helps.

Answer 5

If we go from point A to point B we undergo a displacement. This is the distance from A to B, together with its direction, and is the archetypal vector quantity.

We can give the position of a point as a displacement from some agreed datum point or origin, O.

In your question – which in my opinion is not nicely worded – the motion is presumably along a straight line. Saying that the position at time 0 is 2 m implies a displacement of +2 m from some origin. Your x is the position of the particle at time t, that is its displacement from the origin at time t.

Answer 6

Position and displacement are different, but you will find people use them as synonyms. For school purposes, its important to learn exactly how your textbook and teacher handle these terms and to understand that they are different. When you get out into the real world, you will find context makes it much more obvious what people are talking about, and you can ask for clarification if you need.

Positions are points in space. They are always defined within some coordinate system. Equations of motion are typically phrased in terms of position. There is always exactly one origin for a coordinate system like this, so we can unambiguously identify positions.

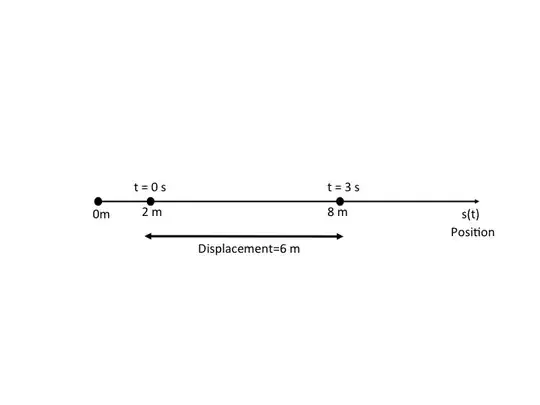
In your example, you are calculating positions. They give you an initial position of x=2m, and you calculate the final position to be x=8m

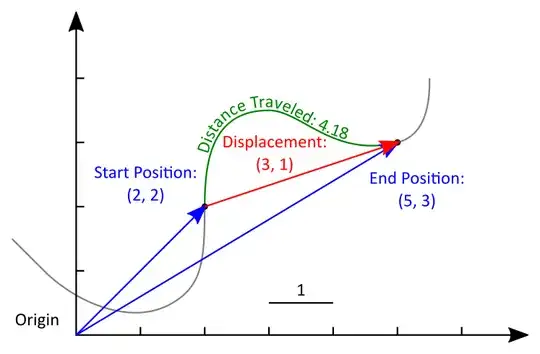
Displacement is a difference in position from some reference point. Most commonly this is the point at t=0, though that may not always be the case. In your example, the most reasonable assumption is that "displacement" means "displacement [from its initial position]." Since it starts at x=2m and ends at x=8m, the total displacement is 8m-2m=6m. If you want to make a displacement clear, the Delta ($\Delta$) symbol is typically used. I might write $\Delta x=6\;\text m$.

Displacement is commonly used when some measurements are more meaningful or easy to describe than others. Consider the movement of a piston up and down. If I have one big coordinate system for the entire engine, the piston may be at y=208mm at "top dead center" and y=186mm at the bottom of its movement. It's much easier for me to say "At the bottom of the stroke, the piston has been displaced 22mm from its position at top dead center" than it is to measure it from some origin. This is especially true if there's variability. There may be 5mm of variability in how high the piston is installed in the engine, but only 1mm of variability in its stroke length. Talking about displacement makes it easy to discard variability you didn't need.

Now comes the confusion. One can always talk about a position as a displacement from an origin. In fact, in some systems this is a far easier approach because it treats points and vectors as one and the same. Likewise, I can always define a reference frame centered on the initial position of an object, and then its position in that frame is the same as its displacement.

This is why the two terms are easy to confuse. While they are different, we will often smoothly flow from one term to another. In the real world, ask questions. In the world of test taking, learn the language hints your textbooks use and pass your tests.

Which brings us to distances. A distance is a length of a line in space. The distance between point A and point B is the length of a line between them. However, we can also talk about the length of arbitrary curves, not just straight lines. This is what your homework problem is trying to do. I believe it was supposed to read "distance traveled," which is the length of the curve tracing the path the object takes.

In your case, the object travels in one direction from t=0 until t=2, when its velocity is zero, then it travels the other direction from t=2 to t=3. Thus the length of this curve is the length between where it was at t=0 and where it was at t=2, plus length between where it was a t=2 and t=3. At t=2, x=10, so the particle has traveld from x=2 to x=10, a distance of 8. Then it travels from x=10 at t=2 to x=8 at t=3, for an additional distance of 2. The total distance traveled will be 10m.

Answer 7

Suppose you start on the 10th step of a very big stair. You walk 100 steps up the stair, then turn around and walk 95 steps down.

• Your position is where you are, which is now the 15th step.
• Your displacement is the net change of your position, which is $15-10=5$ steps.
• Your distance traveled is how much you actually moved, which is $100+95=195$ steps.

In relation to your example:

• If position $x$ at time $t$ is $x(t)$ you can get position at $t_f=3$ s by finding $x(t_f)=x(3\text{ s})$.
• If you started moving at time $t_i$ and finished at $t_f$ then the displacement is the net change in position $\Delta x = x(t_f) - x(t_i)=x(3\text{ s})-x(0\text{ s})$.
• Distance traveled is found by adding up each individual "step". For continuous movements, you must add up infinitely small steps $dx = x(t)dt$, which is given by $\int_{t_i}^{t_f}x(t)dt$. This is what you found.

I will leave the calculations themselves as an exercise to the reader.