Let's do some math, shall we? Fermat's principle is actually a least-time principle. What it says is, that out of all possible trajectories between two points, light is going to follow the one that minimizes the time spent traversing that trajectory.
We know that light travels in straight lines if it's speed is constant throughout the medium, but at the interface of two media where light changes it's propagation speed we assume that we don't know how the light ray is gonna snap (in other words, we have unknown angles of incidence and refraction. We are going to derive Snell's law.
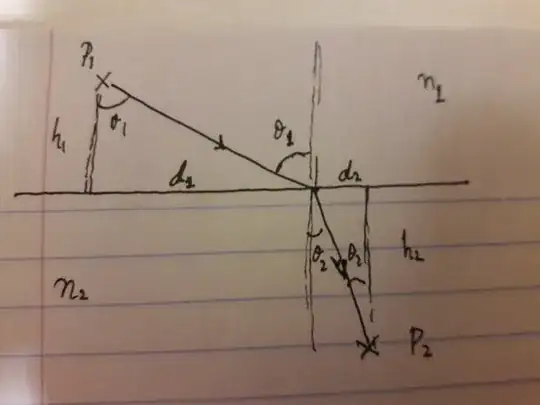
Suppose the light ray is emitted at point $P_1$ and wants to reach point $P_2$ in the least time possible. These points are fixed and their coordinates are $P_1(0,h_1), P_2(-h_2, D)$. Now we would like to minimize the time traversed on the set of possible trajectories. Assume that the light ray is incident distance $d_1$ away from $P_1$ and $d_2$ away from $P_2$. We know that $d_1+d_2=D$. Also the total time of travel between the two points is:
$$T(d_1,d_2)=t_1+t_2=\frac{L_1}{v_1}+\frac{L_2}{v_2}=\frac{1}{c}\Big[n_1\sqrt{d_1^2+h_1^2}+n_2\sqrt{d_2^2+h_2^2}\Big]~~, ~~ d_1+d_2=D$$
Now we want to minimize $T$ under the constraint written above. Using standard Lagrange multipliers procedures we minimize
$$\tilde{T}=T(d_1,d_2)-\lambda(d_1+d_2-D)$$
and we compute
$$\frac{\partial\tilde{T}}{\partial d_1}=\frac{n_1d_1}{c\sqrt{d_1^2+h_1^2}}-\lambda=0\\
\frac{\partial\tilde{T}}{\partial d_2}=\frac{n_2d_2}{c\sqrt{d_2^2+h_2^2}}-\lambda=0$$
Notice that $\sin\theta_1=\frac{d_1}{\sqrt{d_1^2+h_1^2}}$ and similarly for the angle of incidence (just swap index 1 for 2) and thus we get immediately that:
$$n_1\sin\theta_1=n_2\sin\theta_2=\lambda$$
I guess the take away here is what Fermat really says is that along a trajectory the time traversed is minimized. So when some authors say air path length, this actually means time. To understand why they say that, suppose the index of refraction is varying continuously in space. Then we need to minimize
$$T=\int_{trajectory}dt=\int{\frac{ds}{v(s)}}=\frac{1}{c}\int_{P_1\rightarrow P_2}n(x(s), y(s))ds$$
and this can be minimized using standard calculus of variations techniques. The last quantity (maybe omitting the speed of light) is the "path length" that they're talking about, because in the integral the actual path length $ds$ is considered, but weighted by a certain function of spacetime, the index of refraction.
Hope this is helpful!
