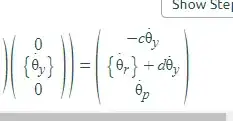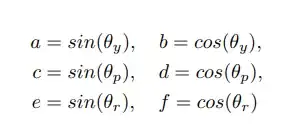Suppose you have a Y-Z-Y scheme with a corresponding sequence of rotation angles $\theta_y$, $\theta_p$ and $\theta_r$.
After the first rotation (yaw), the 3×3 orientation matrix $\mathrm{E}_y$ and angular velocity vector $\vec{\omega}_y$ is
$$\begin{aligned}
\mathrm{E}_y & = \mathrm{rot}(\hat{j}, \theta_y) & \vec{\omega}_y & = \dot{\theta}_y \left(\hat{j}\right)
\end{aligned} \;\tag{1}$$
The above should be self-evident. Now consider the second rotation and the orientation matrix $\mathrm{E}_p$ and angular velocity vector $\vec{\omega}_p$. Since the local axes are rotated by the first rotation we have
$$\begin{aligned}
\mathrm{E}_p & = \mathrm{E}_y \mathrm{rot}(\hat{k}, \theta_p) & \vec{\omega}_p & = \dot{\theta}_y \left( \hat{j} \right) + \dot{\theta}_p \left( \mathrm{E}_y \hat{k} \right)
\end{aligned} \;\tag{2}$$
Finally, with the third rotation we extend this pattern to find the final orientation matrix $\mathrm{E}$ and the final rotation velocity vector $\vec{\omega}$
$$\begin{aligned}
\mathrm{E} & = \mathrm{E}_p \mathrm{rot}(\hat{j}, \theta_r) & \vec{\omega} & = \dot{\theta}_y \left( \hat{j} \right) + \dot{\theta}_p \left( \mathrm{E}_y \hat{k} \right) + \dot{\theta}_r \left( \mathrm{E}_p \hat{j} \right)
\end{aligned} \;\tag{3}$$
The last part is re-written as
$$\begin{aligned}
\mathrm{E} & =\mathrm{rot}(\hat{j}, \theta_y)\mathrm{rot}(\hat{k}, \theta_p) \mathrm{rot}(\hat{j}, \theta_r) & \vec{\omega} & = \dot{\theta}_y \hat{j} + \mathrm{rot}(\hat{j}, \theta_y) \left( \hat{k} \dot{\theta}_p + \mathrm{rot}(\hat{k}, \theta_p) \hat{j} \dot{\theta}_r \right)
\end{aligned} \;\tag{4}$$
This expands out to the following jacobian formulation
$$ \vec{\omega} =
\begin{bmatrix}
0 & \sin(\theta_y) & -\sin(\theta_p)\cos(\theta_y) \\
1 & 0 & \cos(\theta_p) \\
0 & \cos(\theta_y) & \sin(\theta_p) \sin(\theta_y)
\end{bmatrix}
\pmatrix{ \dot{\theta}_y \\ \dot{\theta}_p \\ \dot{\theta}_r }
\;\tag{5}$$