1

I am trying to find gravitational potential energy by integrating the gravitational force:

$$\mathbf{F}(\mathbf{r}) = - \ G \frac{Mm}{|\mathbf{r}|^2} \ \hat{\mathbf{r}}$$

where $\mathbf{r}$ is the vector from the centre of the Earth with mass $M$ towards the point of a mass $m$, and $\hat{\mathbf{r}}$ is the unit vector pointing towards the vector $\mathbf{r}$.

The potential energy at a point of the distance $|\mathbf{r}|$ can be found from

$$U(\mathbf{r}) = -\int_{\infty}^{r} - \ G \frac{Mm}{|\mathbf{r}|^2} \hat{\mathbf{r}} \ \cdot \ d\mathbf{r}$$

Then, removing the minus signs the expression becomes

$$U(\mathbf{r}) = \int_{\infty}^{r} \ G \frac{Mm}{|\mathbf{r}|^2} \hat{\mathbf{r}} \ \cdot \ d\mathbf{r}$$

However, look at the picture below that I drew.

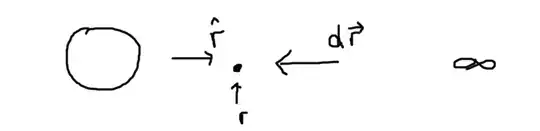enter image description here Since I am integrating from infinity to a point r, I thought $d\mathbf{r}$ should be directed towards the opposite direction of $\hat{\mathbf{r}}$, but actually, if I calculate in that way I get

$$U(\mathbf{r}) = \frac{GMm}{r},$$ in which the minus sign is omitting.

From a mathematical perspective, either of $\hat{\mathbf{r}}$ and $\mathbf{r}$ direct towards the same direction, hence the scalar product should be a positive value.

But I still do not understand why $\hat{\mathbf{r}}$ and $d\mathbf{r}$ should be considered the same direction whenever I am calculating. This is perhaps not accounting for the upper and lower bounds.

Can anybody explain please?

abouttostart
  • 485

1 Answers1

2

First let's do the math. For the path considered in this integral, one has $$ \hat{\bf r} \cdot {\rm d}{\bf r} = {\rm d}r $$ (pay careful attention to use of bold font here: the right hand side is a scalar not a vector). Using this we get $$ U = \int_{\infty}^r GM m \frac{1}{r^2} {\rm d}r = GMm \left[ -\frac{1}{r} \right]^r_{\infty} = - \frac{GMm}{r} $$

I think your worry is understandable, but ${\rm d}{\bf r}$ means the change in $\bf r$, and if this is in the opposite direction to $\bf r$ then this will be taken care of correctly---it will result in ${\rm d}r$ being itself negative, but it is still ${\rm d}r$ not $-{\rm d}r$. That is: $$ \mbox{if } \hat{\bf r} \cdot {\rm d}{\bf r} < 0 \;\mbox{ then } \; {\rm d}r < 0 $$ but this does not change the fact that, for the path under discussion, $$ \hat{\bf r} \cdot {\rm d}{\bf r} = {\rm d}r . $$ (For some other path this relationship would not be true; in general you would have to include the effect of an angle between $\hat{\bf r}$ and ${\rm d}{\bf r}$ that might not be either 0 or 180 degrees.)

Andrew Steane
  • 65,285